Câu hỏi:
3 năm trước
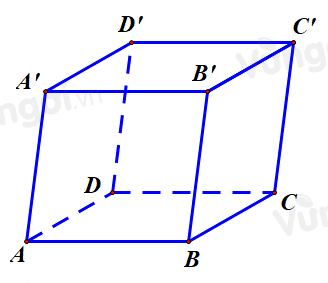
Cho hình lập phương $ABCD.EFGH$ có cạnh bằng $a$ . Tính \(\overrightarrow {AB} .\overrightarrow {EG} .\)
Trả lời bởi giáo viên
Đáp án đúng: b
Ta có \(\overrightarrow {AB} .\overrightarrow {EG} = \overrightarrow {AB} .\overrightarrow {AC} .\) Mặt khác \(\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} \).
Suy ra \(\overrightarrow {AB} .\overrightarrow {EG} = \overrightarrow {AB} .\overrightarrow {AC} = \overrightarrow {AB} \left( {\overrightarrow {AB} + \overrightarrow {AD} } \right) = {\overrightarrow {AB} ^2} + \overrightarrow {AB} .\overrightarrow {AD} \).
Vì \(ABCD\) là hình vuông \( \Rightarrow AB \bot AD \Leftrightarrow \overrightarrow {AB} .\overrightarrow {AD} = 0\)
\( \Rightarrow {\overrightarrow {AB} ^2} + \overrightarrow {AB} .\overrightarrow {AD} = A{B^2} + 0 = {a^2}.\)
Hướng dẫn giải:
Biểu diễn véc tơ \(\overrightarrow {EG} \) qua các véc tơ không đồng phẳng có giá là các cạnh của hình lập phương, từ đó tính tích vô hướng.
