Trả lời bởi giáo viên
Đáp án đúng: c

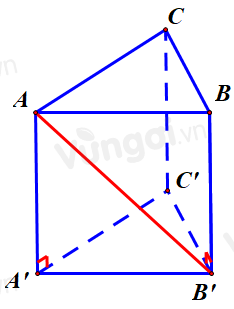
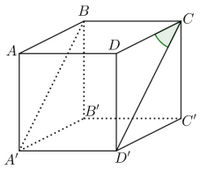
Gọi \(a\) là độ dài cạnh hình lập phương. Khi đó, tam giác \(AB'C\) đều (\(AB' = B'C = CA = a\sqrt 2 \)) do đó \(\widehat {B'CA} = {60^0}\).
Lại có, \(DA'\) song song \(CB'\) nên \(\left( {AC,DA'} \right) = \left( {AC,CB'} \right) = \widehat {ACB'} = {60^0}.\)
Hướng dẫn giải:
Sử dụng mối quan hệ song song giữa các đường thẳng và kiến thức hình học đã biết để xác định góc giữa hai đường thẳng bài yêu cầu.