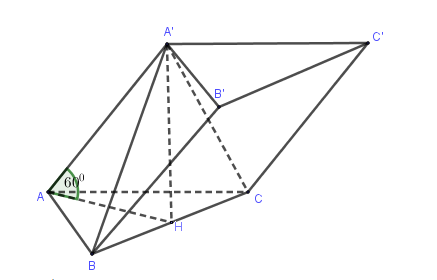
Cho hình lăng trụ tam giác \(ABC.A'B'C'\) có cạnh bên bằng $a.$ Các cạnh bên của lăng trụ tạo với mặt đáy góc ${60^{\rm{o}}}.$ Hình chiếu vuông góc của $A'$ lên mặt phẳng $\left( {ABC} \right)$ là trung điểm của $BC$. Khoảng cách giữa hai mặt đáy của lăng trụ bằng bao nhiêu?

$a\sqrt 2 .$ 

$a\sqrt 3 .$

$2a.$

$a.$

$a$.

$a\sqrt 2 $.

$\dfrac{{a\sqrt 3 }}{2}$.

$\dfrac{{2a}}{3}$.

Nếu \(a\) và $b$ cùng vuông góc với $c$  thì $a//b$ 

Nếu $a//b$ và \(c \bot a\) thì \(c \bot b\).

Nếu góc giữa $a$ và $c$ bằng góc giữa $b$ và $c$ thì $a//b$. 

Nếu $a$ và $b$ cùng nằm trong $mp\left( \alpha  \right)//c~$ thì góc giữa $a$ và $c$ bằng góc giữa $b$ và $c$.

Đường vuông góc chung của hai đường thẳng chéo nhau thì vuông góc với mặt phẳng chứa đường thẳng này và song song với đường thẳng kia

Một đường thẳng là đường vuông góc chung của hai đường thẳng chéo nhau nếu nó vuông góc với cả hai đường thẳng đó

Đường vuông góc chung của hai đường thẳng chéo nhau thì nằm trong mặt phẳng chứa đường thẳng này và vuông góc với đường thẳng kia

Một đường thẳng là đường vuông góc chung của hai đường thẳng chéo nhau nếu nó cắt cả hai đường thẳng đó.

\(a\sqrt 2 \).

\(\dfrac{{a\sqrt 6 }}{2}\).

\(\dfrac{{a\sqrt 3 }}{2}\).

\(a\sqrt 3 \).

\(\left| {\vec a + \vec b} \right| = \sqrt {19} \) 

\(\left| {\vec a - \vec b} \right| = 7\)

\(\left| {\vec a - 2\vec b} \right| = \sqrt {139} \)

\(\left| {\vec a + 2\vec b} \right| = 9\)

\(AB \bot \left( {ABC} \right)\).

\(AC \bot BD\).

\(CD \bot \left( {ABD} \right)\).

\(BC \bot AD\).