Câu hỏi:
3 năm trước
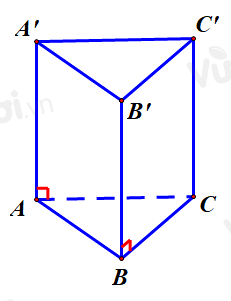
Cho hình lăng trụ đứng \(ABC \cdot {A^\prime }{B^\prime }{C^\prime }\) có đáy $A B C$ là tam giác vuông cân tại \(B\) và \(AB = 4\) (tham khảo hình bên). Khoảng cách từ \(C\) đến mặt phẳng \(\left( {AB{B^\prime }{A^\prime }} \right)\) bằng
Trả lời bởi giáo viên
Đáp án đúng: d
Ta có
\(\left. {\begin{array}{*{20}{l}}{CB \bot B{B^\prime }}\\{CB \bot AB}\end{array}} \right\} \Rightarrow CB \bot \left( {AB{B^\prime }{A^\prime }} \right)\)
Vậy \(d\left( {C;\left( {AB{B^\prime }{A^\prime }} \right)} \right) = CB = AB = 4\)
Hướng dẫn giải:
- Chứng minh BC vuông góc với (ABB’A’)
- Tính \(d\left( {C;\left( {AB{B^\prime }{A^\prime }} \right)} \right)\)