Cho hình lăng trụ \(ABC \cdot {A^\prime }{B^\prime }{C^\prime }\) có đáy là tam giác đều cạnh $3 a$, hình chiếu của \({A^\prime }\) trên mặt phẳng \((ABC)\) trùng với tâm đường tròn ngoại tiếp tam giác $ABC$. Cạnh \({\rm{AA'}}\) hợp với mặt phẳng đáy một góc \({45^\circ }\). Thể tích của khối lăng trụ \(ABC \cdot {A^\prime }{B^\prime }{C^\prime }\) tính theo \(a\) bằng.
Trả lời bởi giáo viên
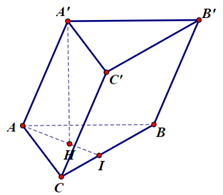
Gọi $AI$ là đường cao, \(H\) là tâm của tam giác \(ABC \Rightarrow {A^\prime }H \bot (ABC)\).
Vì \(\left\{ {\begin{array}{*{20}{l}}{A{A^\prime } \cap (ABC) = A}\\{{A^\prime }H \bot (ABC)}\end{array} \Rightarrow } \right.\) góc giữa \(A{A^\prime }\) và \((ABC)\) là \(\widehat {{A^\prime }AH} \Rightarrow \widehat {{A^\prime }AH} = {45^\circ }\).
Ta có: \(AI = \dfrac{{3a\sqrt 3 }}{2},AH = \dfrac{2}{3}AI = a\sqrt 3 ,{S_{ABC}} = \dfrac{{{{(3a)}^2}\sqrt 3 }}{4} = \dfrac{{9{a^2}\sqrt 3 }}{4}\). \({A^\prime }H = AH \cdot \tan {45^\circ } = AH = a\sqrt 3 .\)
Thể tích của lăng trụ là:
\(V = {A^\prime }H \cdot {S_{ABC}} = a\sqrt 3 \cdot \dfrac{{9{a^2}\sqrt 3 }}{4} = \dfrac{{27{a^3}}}{4}{\rm{. }}\)
Hướng dẫn giải:
Kẻ đường cao và lấy tâm H của tam giác ABC.
\( \Rightarrow V = {A^\prime }H \cdot {S_{ABC}}\)
Câu hỏi khác
- Đề thi ĐGNL Hà Nội - Đề số 1 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 2 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 10 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 9 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 7 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
