Cho hình chóp tứ giác đều S.ABCD có cạnh đáy và cạnh bên đều bằng a. Tính cosin của góc giữa hai mặt phẳng (SAB) và (SAD)

Chỉ được phép điền số 0, nguyên âm, nguyên dương và phân số dạng a/b

Đáp án:

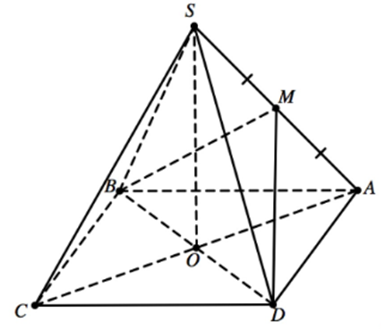
Gọi M là trung điểm của cạnh SA.

Do SAB và SAD là các tam giác đều nên ta có:

\(\left. \begin{array}{l}BM \bot SA\\DM \bot SA\end{array} \right\}\)\( \Rightarrow \widehat {\left( {\left( {SAB} \right),\left( {SAD} \right)} \right)} = \widehat {\left( {BM,DM} \right)} = \widehat {BMD}\)

Do tam giác SAB đều nên ta có \(BM = \dfrac{{AB\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{2}\)

Tam giác SAD đều nên ta có \(DM = \dfrac{{AD\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{2}\)

S.ABCD là hình chóp tứ giác đều nên ABCD là hình vuông cạnh AB=a

=>\(BD = AB\sqrt 2  = a\sqrt 2 \)

Tam giác BDM có:

\(\cos \widehat {BMD} = \dfrac{{M{B^2} + M{D^2} - B{D^2}}}{{2.MB.MD}}\)\( = \dfrac{{{{\left( {\dfrac{{\sqrt 3 }}{2}a} \right)}^2} + {{\left( {\dfrac{{\sqrt 3 }}{2}a} \right)}^2} - {{\left( {\sqrt 2 a} \right)}^2}}}{{2.\left( {\dfrac{{\sqrt 3 }}{2}a} \right)\left( {\dfrac{{\sqrt 3 }}{2}a} \right)}} =  - \dfrac{1}{3}\)

Do đó \(\cos \widehat {\left( {\left( {SAB} \right),\left( {SAD} \right)} \right)} = \dfrac{1}{3}\) (do góc giữa hai mặt phẳng phải không lớn hơn \({90^0}\)).