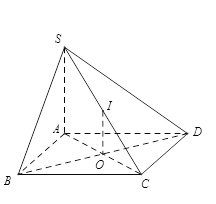
Cho hình chóp \(S.ABCD\) có \(SA \bot \left( {ABCD} \right)\) và đáy \(ABCD\) là hình chữ nhật. Gọi \(O\) là tâm của \(ABCD\) và \(I\) là trung điểm của \(SC\). Khẳng định nào sau đây sai ?
Trả lời bởi giáo viên
Có \(IO\) là đường trung bình tam giác \(SAC\) nên \(IO//SA\) nên \(IO \bot \left( {ABCD} \right)\) nên A đúng.
Có \(\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\end{array} \right. \Rightarrow BC \bot SB\) nên B đúng
Và \(\left\{ \begin{array}{l}CD \bot AD\\CD \bot SA\end{array} \right. \Rightarrow CD \bot SD\) nên phương án D đúng.
Đáp án C sai vì nếu \(\left( {SAC} \right)\) là mặt phẳng trung trực của \(BD\) \( \Rightarrow BD \bot AC\)(vô lý).
Hướng dẫn giải:
Sử dụng điều kiện đường thẳng vuông góc mặt phẳng và định nghĩa mặt phẳng trung trực để xét tính đúng, sai của từng đáp án.

