Cho hình chóp $S.ABCD$ có đáy là hình thoi cạnh bằng $2$, $\angle BAD = {60^0}$, $SA = SC$ và tam giác $SBD$ vuông cân tại $S$. Gọi $E$ là trung điểm của $SC$. Mặt phẳng $\left( P \right)$ qua $AE$ và cắt hai cạnh $SB,\,\,SD$ lần lượt tại $M$ và $N$. Thể tích lớn nhất ${V_0}$ của khối đa diện $ABCDNEM$ bằng:

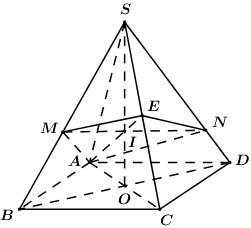
Gọi $O = AC \cap BD$, ta có:

$SA = SC \Rightarrow \Delta SAC$ cân tại $S$ $\Rightarrow SO \bot AC$.

Tam giác $SBD$ vuông cân tại $S$ $\Rightarrow SO \bot BD$.

$\Rightarrow SO \bot \left( {ABCD} \right)$.

Trong $\left( {SBD} \right)$, gọi $I = MN \cap BD$.

Đặt $\dfrac{{SM}}{{SB}} = x,\,\,\dfrac{{SN}}{{SD}} = y\,\,\left( {0 < x,\,\,y < 1} \right)$.

Ta có: $\dfrac{{{V_{S.AME}}}}{{{V_{S.ABC}}}} = \dfrac{{SM}}{{SB}}.\dfrac{{SE}}{{SC}} = \dfrac{1}{2}x \Rightarrow \dfrac{{{V_{S.AME}}}}{{{V_{S.ABCD}}}} = \dfrac{1}{4}x$, $\dfrac{{{V_{S.ANE}}}}{{{V_{S.ADC}}}} = \dfrac{{SN}}{{SD}}.\dfrac{{SE}}{{SC}} = \dfrac{1}{2}y \Rightarrow \dfrac{{{V_{S.ANE}}}}{{{V_{S.ABCD}}}} = \dfrac{1}{4}y$.

$\Rightarrow \dfrac{{{V_{S.AMNE}}}}{{{V_{S.ABCD}}}} = \dfrac{{{V_{S.AME}}}}{{{V_{S.ABCD}}}} + \dfrac{{{V_{S.ANE}}}}{{{V_{S.ABCD}}}} = \dfrac{{x + y}}{4}\,\,\,\left( 1 \right)$.

Ta lại có: $\dfrac{{{V_{S.AMN}}}}{{{V_{S.ABD}}}} = \dfrac{{SM}}{{SA}}.\dfrac{{SN}}{{SD}} = xy \Rightarrow \dfrac{{{V_{S.AMN}}}}{{{V_{S.ABCD}}}} = \dfrac{{xy}}{2}$, $\dfrac{{{V_{S.MNE}}}}{{{V_{S.BDC}}}} = \dfrac{{SM}}{{SB}}.\dfrac{{SN}}{{SD}}.\dfrac{{SE}}{{SC}} = \dfrac{1}{2}xy \Rightarrow \dfrac{{{V_{S.MNE}}}}{{{V_{S.ABCC}}}} = \dfrac{{xy}}{4}$.

$\Rightarrow \dfrac{{{V_{S.AMNE}}}}{{{V_{S.ABCD}}}} = \dfrac{{{V_{S.AMN}}}}{{{V_{S.ABCD}}}} + \dfrac{{{V_{S.MNE}}}}{{{V_{S.ABCD}}}} = \dfrac{{xy}}{2} + \dfrac{{xy}}{4} = \dfrac{{3xy}}{4}\,\,\left( 2 \right)$.

Từ (1) và (2) $\Rightarrow \dfrac{{x + y}}{4} = \dfrac{{3xy}}{4} \Leftrightarrow x + y = 3xy$$\Leftrightarrow x = \left( {3x - 1} \right)y \Leftrightarrow y = \dfrac{x}{{3x - 1}}\,\,\left( {x \ne \dfrac{1}{3}} \right)$.

Do $x,\,\,y > 0 \Rightarrow 3x - 1 > 0 \Leftrightarrow x > \dfrac{1}{3}$.

Khi đó ta có $\dfrac{{{V_{S.AMNE}}}}{{{V_{S.ABCD}}}} = \dfrac{1}{4}\left( {x + \dfrac{x}{{3x - 1}}} \right)$.

Xét hàm số $f\left( x \right) = x + \dfrac{x}{{3x - 1}}\,\,\left( {x > \dfrac{1}{3}} \right)$ ta có:

$f'\left( x \right) = 1 - \dfrac{1}{{{{\left( {3x - 1} \right)}^2}}} = 0$ $\Leftrightarrow \left[ \begin{array}{l}3x - 1 = 1\\3x - 1 =  - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{2}{3}\\x = 0\,\,\,\left( {ktm} \right)\end{array} \right.$

BBT:

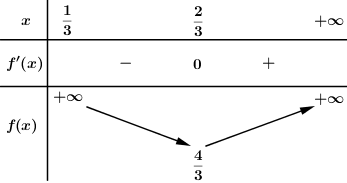
Dựa vào BBT ta thấy $\min {V_{S.AMNE}} = \dfrac{1}{4}.\dfrac{4}{3}{V_{S.ABCD}} = \dfrac{1}{3}{V_{S.ABCD}}$ $\Rightarrow \max {V_{ABCDNEM}} = \dfrac{2}{3}{V_{S.ABCD}} \Rightarrow {V_0} = \dfrac{2}{3}{V_{S.ABCD}}$.

Ta có: $\Delta ABD$ đều cạnh 2 $\left( {AB = AD,\,\angle BAD = {{60}^0}} \right)$ $\Rightarrow {S_{ABD}} = \dfrac{{{2^2}\sqrt 3 }}{4} = \sqrt 3$ $\Rightarrow {S_{ABCD}} = 2\sqrt 3$.

Tam giác $ABD$ đều cạnh 2 $\Rightarrow$$BD = 2$, lại có tam giác $SBD$ vuông cân tại $S$ nên $SO = \dfrac{1}{2}BD = 1$.

$\Rightarrow {V_{S.ABCD}} = \dfrac{1}{3}SO.{S_{ABCD}} = \dfrac{1}{3}.1.2\sqrt 3  = \dfrac{{2\sqrt 3 }}{3}$.

Vậy  ${V_0} = \dfrac{2}{3}{V_{S.ABCD}} = \dfrac{{4\sqrt 3 }}{9}$.