Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, \(AB = a,\) \(AD = 2a\). Tam giác \(SAB\) cân tại \(S\) và nằm trong mặt phẳng vuông góc với đáy. Góc giữa \(SC\) và mặt phẳng \(\left( {ABCD} \right)\) bằng \({45^0}\). Gọi \(M\) là trung điểm \(SD\), hãy tính theo \(a\) khoảng cách \(d\) từ \(M\) đến mặt phẳng \(\left( {SAC} \right)\).
Đáp án:
Trả lời bởi giáo viên
Đáp án:
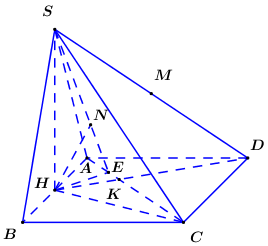
Bước 1: Đổi \(d\left( {M;\left( {SAC} \right)} \right)\) sang \(d\left( {H;\left( {SAC} \right)} \right)\).
Gọi \(H\) là trung điểm \(AB\). Vì \(\Delta SAB\) cân tại \(S\) nên \(SH \bot AB\).
Ta có: \(\left\{ \begin{array}{l}\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\\SH \subset \left( {ABCD} \right),\,\,SH \bot AB\end{array} \right.\) \( \Rightarrow SH \bot \left( {ABCD} \right)\).
Gọi \(K = HD \cap AC\). Áp dụng định lí Ta-let ta có \(\dfrac{{DK}}{{HK}} = \dfrac{{DC}}{{AH}} = 2 \Rightarrow DK = 2HK\).
Ta có \(MD \cap \left( {SAC} \right) = S \Rightarrow \dfrac{{d\left( {M;\left( {SAC} \right)} \right)}}{{d\left( {D;\left( {SAC} \right)} \right)}} = \dfrac{{SM}}{{SD}} = \dfrac{1}{2}\)
\( \Rightarrow d\left( {M;\left( {SAC} \right)} \right) = \dfrac{1}{2}d\left( {D;\left( {SAC} \right)} \right)\)
Lại có \(DH \cap \left( {SAC} \right) = K\) nên \(\dfrac{{d\left( {D;\left( {SAC} \right)} \right)}}{{d\left( {H;\left( {SAC} \right)} \right)}} = \dfrac{{DK}}{{HK}} = 2 \Rightarrow d\left( {D;\left( {SAC} \right)} \right) = 2d\left( {H;\left( {SAC} \right)} \right)\)
Bước 2: Trong \(\left( {ABCD} \right)\) kẻ \(HE \bot AC\,\,\left( {E \in AC} \right)\), trong \(\left( {SHE} \right)\) kẻ \(HN \bot SE\,\,\left( {N \in SE} \right)\), chứng minh \(HN \bot \left( {SAC} \right)\)
Do đó \(d\left( {M;\left( {SAC} \right)} \right) = d\left( {H;\left( {SAC} \right)} \right)\)
Trong \(\left( {ABCD} \right)\) kẻ \(HE \bot AC\,\,\left( {E \in AC} \right)\), trong \(\left( {SHE} \right)\) kẻ \(HN \bot SE\,\,\left( {N \in SE} \right)\) ta có:
\(\left\{ \begin{array}{l}AC \bot HE\\AC \bot SH\end{array} \right. \Rightarrow AC \bot \left( {SHE} \right) \)\(\Rightarrow AC \bot HN\)\(\left\{ \begin{array}{l}HN \bot SE\\HN \bot AC\end{array} \right. \Rightarrow HN \bot \left( {SAC} \right)\)\( \Rightarrow d\left( {H;\left( {SAC} \right)} \right) = HN\)
Bước 3: Xác định góc giữa \(SC\) và \(\left( {ABCD} \right)\), từ đó tính \(SH\).
Vì \(SH \bot \left( {ABCD} \right)\) nên \(HC\) là hình chiếu vuông góc của \(SC\) lên \(\left( {ABCD} \right)\)
\( \Rightarrow \angle \left( {SC;\left( {ABCD} \right)} \right) = \angle \left( {SC;HC} \right) = \angle SCH = {45^0}\)
\( \Rightarrow \Delta SHC\) vuông cân tại \(H\)\( \Rightarrow SH = HC = \sqrt {B{C^2} + B{H^2}} \)\(= \sqrt {{{\left( {2a} \right)}^2} + {{\left( {\dfrac{a}{2}} \right)}^2}} = \dfrac{{a\sqrt {17} }}{2}\)
Bước 4: Tính \(d\left( {M;\left( {SAC} \right)} \right) \)
Ta có: \({S_{HAC}} = \dfrac{1}{2}HE.AC = \dfrac{1}{2}{S_{ABC}}\)
$\Rightarrow HE.AC = \dfrac{1}{2}.AB.BC$
$ \Rightarrow HE = \dfrac{{\dfrac{1}{2}.AB.BC}}{{AC}} $$= \dfrac{{\dfrac{1}{2}.a.2a}}{{\sqrt {{a^2} + {{\left( {2a} \right)}^2}} }} $$= \dfrac{a}{{\sqrt 5 }}$
Áp dụng hệ thức lượng trong tam giác vuông \(SHE\) ta có:
Nên \(HN = \dfrac{{SH.HE}}{{\sqrt {S{H^2} + H{E^2}} }} = \dfrac{{\dfrac{{a\sqrt {17} }}{2}.\dfrac{a}{{\sqrt 5 }}}}{{\sqrt {\dfrac{{17{a^2}}}{4} + \dfrac{{{a^2}}}{5}} }} = \dfrac{{a\sqrt {1513} }}{{89}}\)
Vậy \(d\left( {M;\left( {SAC} \right)} \right) = \dfrac{{a\sqrt {1513} }}{{89}}\).
Hướng dẫn giải:
Bước 1: Đổi \(d\left( {M;\left( {SAC} \right)} \right)\) sang \(d\left( {H;\left( {SAC} \right)} \right)\).
Bước 2: Trong \(\left( {ABCD} \right)\) kẻ \(HE \bot AC\,\,\left( {E \in AC} \right)\), trong \(\left( {SHE} \right)\) kẻ \(HN \bot SE\,\,\left( {N \in SE} \right)\), chứng minh \(d\left( {H;\left( {SAC} \right)} \right) = HN\)
Bước 3: Xác định góc giữa \(SC\) và \(\left( {ABCD} \right)\), từ đó tính \(SH\).
Bước 4: Tính \(d\left( {M;\left( {SAC} \right)} \right) \)
- Sử dụng \({S_{HAC}} = \dfrac{1}{2}HE.AC = \dfrac{1}{2}{S_{ABC}}\), từ đó tính \(HE\).
- Sử dụng hệ thức lượng trong tam giác vuông tính \(HN\).