Câu hỏi:
2 năm trước
Cho hình chóp $S.ABC$ có đáy $\widehat {BAC} = {90^0},\,\,\,BC = 2a,\,\,\,\widehat {ACB} = {30^0}.$ Mặt phẳng $\left( {SAB} \right)$ vuông góc với mặt phẳng $\left( {ABC} \right).$ Biết rằng tam giác $SAB$ cân tại $S$ và tam giác $SBC$ vuông tại $S.$ Tính diện tích tam giác $SAB.$
Trả lời bởi giáo viên
Đáp án đúng: c
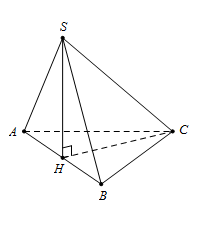
Gọi $H$ là trung điểm của $AB,$ tam giác $SAB$ cân tại $S \Rightarrow SH \bot AB.$
Mà $\left( {SAB} \right) \bot \left( {ABC} \right)$ nên $SH \bot \left( {ABC} \right)$ và đặt $SH = x.$
Tam giác $ABC$ vuông tại $A$ có $\left\{ \begin{array}{l}AB = BC.\sin C = a\\AC = BC.\cos C = a\sqrt 3 \end{array} \right..$
Ta có $SB = \sqrt {S{H^2} + H{B^2}} = \sqrt {{x^2} + \dfrac{{{a^2}}}{4}} ,$ $HC = \sqrt {H{A^2} + A{C^2}} = \dfrac{{a\sqrt {13} }}{2}$
Và $SC = \sqrt {S{H^2} + H{C^2}} = \sqrt {{x^2} + \dfrac{{13{a^2}}}{4}} $
Tam giác SBC vuông tại S nên $S{B^2} + S{C^2} = B{C^2}$
$ \Leftrightarrow {x^2} + \dfrac{{{a^2}}}{4} + {x^2} + \dfrac{{13\,{a^2}}}{4} = 4{a^2} \Leftrightarrow {x^2} = \dfrac{{{a^2}}}{4}$$ \Leftrightarrow x = \dfrac{a}{2} \Rightarrow SH = \dfrac{a}{2}.$
Vậy diện tích tam giác $SAB$ là ${S_{\Delta \,SAB}} = \dfrac{1}{2}.SH.AB = \dfrac{{{a^2}}}{4}.$
