Cho hình chóp $S . A B C D$ có đáy là hình bình hành và có thề tích là \(V\). Điềm \(P\) là trung điểm của $S C$, một mặt phẳng qua $A P$ cắt các cạnh $S D$ và $S B$ lần lượt tại \(M\) và \(N\). Gọi \({V_1}\) là thể tích khối chóp $S . A M P N$. Tìm giá trị nhỏ nhất của \(\dfrac{{{V_1}}}{V}\) ?

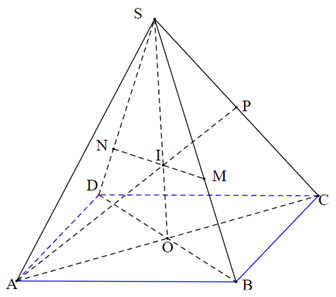
Đặt \(\dfrac{{SM}}{{SB}} = x,\dfrac{{SN}}{{SD}} = y,0 < x,y \le 1\).

Vì \(\dfrac{{SA}}{{SA}} + \dfrac{{SC}}{{SP}} = \dfrac{{SB}}{{SM}} + \dfrac{{SD}}{{SN}}\) nên:

\(1 + 2 = \dfrac{1}{x} + \dfrac{1}{y} \Rightarrow y = \dfrac{x}{{3x - 1}}\)

Khi đó:

 \(\dfrac{{{V_1}}}{V} = \dfrac{{{V_{S.ANP}}}}{{2{V_{S.ADC}}}} + \dfrac{{{V_{S.A \cdot MP}}}}{{2{V_{S.ABC}}}} = \dfrac{1}{2} \cdot \dfrac{{SA}}{{SA}} \cdot \dfrac{{SN}}{{SD}} \cdot \dfrac{{SP}}{{SC}} + \dfrac{1}{2} \cdot \dfrac{{SA}}{{SA}} \cdot \dfrac{{SM}}{{SB}} \cdot \dfrac{{SP}}{{SC}} = \dfrac{1}{2} \cdot y \cdot \dfrac{1}{2} + \dfrac{1}{2} \cdot x \cdot \dfrac{1}{2}\) \( = \dfrac{1}{4}(x + y) = \dfrac{1}{4}\left( {x + \dfrac{x}{{3x - 1}}} \right)\)

Vì \(x > 0,y > 0\) nên \(\dfrac{1}{3} < x < 1\)

Xét hàm số \(f(x) = \dfrac{1}{4}\left( {x + \dfrac{x}{{3x - 1}}} \right)\) trên \(\left( {\dfrac{1}{3};1} \right]\)

Ta có \({f^\prime }(x) = \dfrac{1}{4}\left( {1 - \dfrac{1}{{{{(3x - 1)}^2}}}} \right);{f^\prime }(x) = 0 \Leftrightarrow x = \dfrac{2}{3}\).

Bảng biến thiên

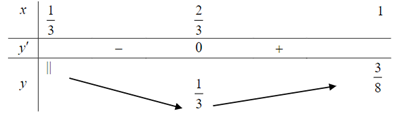
Vậy giá trị nhỏ nhất của \(\dfrac{{{V_1}}}{V}\) bằng \(\dfrac{1}{3}\).