Câu hỏi:
2 năm trước
Cho hệ bất phương trình \(\left\{ \begin{array}{l}2x - \dfrac{3}{2}y \ge 1\\4x - 3y \le 2\end{array} \right.\) có tập nghiệm \(S\). Khẳng định nào sau đây là khẳng định đúng?
Trả lời bởi giáo viên
Đáp án đúng: b
Dễ thấy \(x = - \dfrac{1}{4};y = - 1\) thỏa mãn cả hai bất phương trình nên \(\left( { - \dfrac{1}{4}; - 1} \right) \in S\), do đó A sai.
Ta sẽ biểu diễn tập nghiệm của bất phương trình trên mặt phẳng tọa độ như sau:
Trước hết, ta vẽ hai đường thẳng:
\(\left( {{d_1}} \right):2x - \dfrac{3}{2}y = 1\)
\(\left( {{d_2}} \right):4x - 3y = 2\)
Thử trực tiếp ta thấy \(\left( {0\,\,;\,\,0} \right)\) là nghiệm của bất phương trình (2) vì 4.0-3.0 < 2 (đúng)
Nhưng (0;0) không phải là nghiệm của bất phương trình (1) vì \(2.0 - \dfrac{3}{2}.0 < 1\).
Sau khi gạch bỏ các miền không thích hợp, tập hợp nghiệm của bất phương trình chính là các điểm thuộc đường thẳng \(\left( d \right):4x - 3y = 2.\)
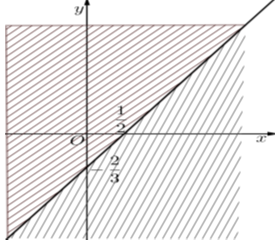
Hướng dẫn giải:
- Biểu diễn miền nghiệm của hệ trên mặt phẳng tọa độ.
- Xét tính đúng, sai của từng đáp án và kết luận.
