Cho hàm số $y = \dfrac{{ - {x^2} + 3x + 6}}{{x + 2}}$, chọn kết luận đúng:
Đồ thị hàm số có điểm cực tiểu $\left( { - 4;11} \right)$ và điểm cực đại $\left( {0;3} \right)$.
Trả lời bởi giáo viên
Ta có: $y = \dfrac{{ - {x^2} + 3x + 6}}{{x + 2}} = - x + 5 - \dfrac{4}{{x + 2}}$.
TXĐ: $D = R\backslash \left\{ { - 2} \right\}$.
Ta có: $y' = - 1 + \dfrac{4}{{{{\left( {x + 2} \right)}^2}}} = \dfrac{{ - {x^2} - 4x}}{{{{\left( {x + 2} \right)}^2}}};y' = 0 \Leftrightarrow \left[ \begin{gathered}x = 0 \Rightarrow y = 3 \hfill \\ x = - 4 \Rightarrow y = 11 \hfill \\ \end{gathered} \right.$
Bảng biến thiên:
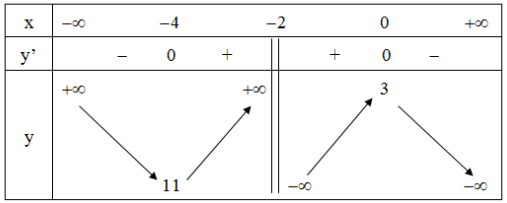
Từ bảng biến thiên ta thấy đồ thị hàm số có điểm cực đại là $\left( {0;3} \right)$ và điểm cực tiểu là $\left( { - 4;11} \right)$.
Hướng dẫn giải:
Tìm cực trị của hàm số theo quy tắc 1:
- Bước 1: Tìm tập xác định của hàm số.
- Bước 2: Tính $f'\left( x \right)$, tìm các điểm tại đó $f'\left( x \right) = 0$ hoặc không xác định.
- Bước 3: Lập bảng biến thiên và kết luận.
+ Tại các điểm mà đạo hàm đổi dấu từ âm sang dương thì đó là điểm cực tiểu của hàm số.
+ Tại các điểm mà đạo hàm đổi dấu từ dương sang âm thì đó là điểm cực đại của hàm số

