Cho hàm số \(y = f\left( x \right)\). Hàm số \(y = f'\left( x \right)\) có bảng biến thiên như sau

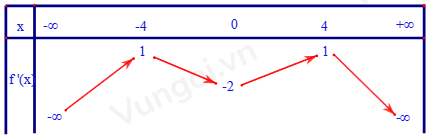
Số điểm cực trị của hàm số \(y = f\left( {{{\left( {{x^4} + 3{x^2} + 2} \right)}^2}} \right) + \left( {{x^4} + 3{x^2} + 1} \right)\left( {{x^4} + 3{x^2} + 3} \right)\) là

Đặt \({\left( {{x^4} + 3{x^2} + 2} \right)^2} = t\)\( \Rightarrow \left( {{x^4} + 3{x^2} + 1} \right)\left( {{x^4} + 3{x^2} + 3} \right) = t - 1\)

\(y = f\left( t \right) + t - 1\)

\(\begin{array}{l}y = f\left( {{{\left( {{x^4} + 3{x^2} + 2} \right)}^2}} \right) + \left( {{x^4} + 3{x^2} + 1} \right)\left( {{x^4} + 3{x^2} + 3} \right)\\y' = t'\left( x \right)\left[ {f'\left( t \right) + 1} \right]\\ = 2.\left( {{x^4} + 3{x^2} + 2} \right)\left( {4{x^3} + 6x} \right)\left[ {f'\left( t \right) + 1} \right]\\y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\f'\left( t \right) + 1 = 0\left( * \right)\end{array} \right.\end{array}\)

\(y' = 0 \Leftrightarrow f'\left( t \right) =  - 1\)

Ta lại có: \({x^4} + 3{x^2} + 2 \ge 2 \Rightarrow t \ge 4\)

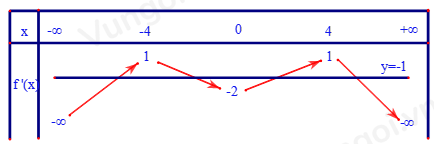
Từ bảng biến thiên, đường thẳng y=-1 cắt đồ thị hàm số \(y = f'\left( t \right)\) tại 1 điểm duy nhất

\(\begin{array}{l}t = a > 4\\ \Leftrightarrow {\left( {{x^4} + 3{x^2} + 2} \right)^2} = a > 4\\ \Leftrightarrow \left[ \begin{array}{l}{x^4} + 3{x^2} + 2 = \sqrt a  > 2\left( 1 \right)\\{x^4} + 3{x^2} + 2 =  - \sqrt a  <  - 2\left( {VN} \right)\end{array} \right.\\\left( 1 \right) \Leftrightarrow {x^4} + 3{x^2} + 2 - \sqrt a  = 0\\{x^2} = u\end{array}\)

Khi đó phương trình trên trở thành

\(\begin{array}{l}{u^2} + 3u + 2 - \sqrt a  = 0\left( 2 \right)\\2 - \sqrt a  < 0\end{array}\)

Nên phương trình (2) có 2 nghiệm trái dấu khác 0.

Hay phương trình (1) có 2 nghiệm phân biệt.

Vậy phương trình đã cho có 3 cực trị.