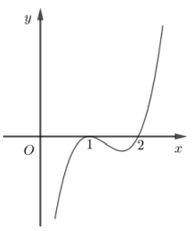
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình bên:

Hàm số \(y = - 2f\left( x \right)\) đồng biến trên khoảng:
Trả lời bởi giáo viên
Dựa vào đồ thị hàm số ta có hàm số \(y = f\left( x \right)\) đồng biến trên các khoảng \(\left( { - \infty ;\,0} \right)\) và \(\left( {2;\, + \infty } \right).\)
Hàm số \(y = f\left( x \right)\) nghịch biến trên \(\left( {0;\,\,2} \right).\)
Xét hàm số: \(y = - 2f\left( x \right)\) ta có: \(y' = - 2f'\left( x \right).\)
Hàm số đồng biến \( \Leftrightarrow - 2f'\left( x \right) \ge 0 \Leftrightarrow f'\left( x \right) \le 0 \Leftrightarrow 0 \le x \le 2.\)
Vậy hàm số \(y = - 2f\left( x \right)\) đồng biến \( \Leftrightarrow x \in \left[ {0;\,2} \right].\)
Hướng dẫn giải:
Dựa vào đồ thị hàm số suy ra các khoảng đồng biến và nghịch biến của hàm số \(y = f\left( x \right)\) từ đó suy ra tính đồng biến và nghịch biến của hàm số \(y = - 2f\left( x \right).\)