Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'(x)\) có đồ thị như hình dưới đây

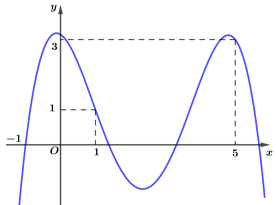
Số điểm cực trị của hàm số \(g\left( x \right) = 8f\left( {{x^3} - 3x + 3} \right) \) \(-\left( {2{x^6} - 12{x^4} + 16{x^3} + 18{x^2} - 48x + 1} \right)\) là:

Ta có:

\(\begin{array}{l}g'\left( x \right) = 8\left( {3{x^2} - 3} \right)f'\left( {{x^3} - 3x + 3} \right) \\- \left( {12{x^5} - 48{x^3} + 48{x^2} + 36x - 48} \right)\\g'\left( x \right) = 24\left( {{x^2} - 1} \right)\left[ {f'\left( {{x^3} - 3x + 3} \right) - \dfrac{1}{2}\left( {{x^3} - 3x + 3 + 1} \right)} \right]\\g'\left( x \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x =  \pm 1\\f'\left( {{x^3} - 3x + 3} \right) = \dfrac{1}{2}\left( {{x^3} - 3x + 3 + 1} \right)\,\,\,\left( * \right)\end{array} \right.\end{array}\)

Đặt \(t = {x^3} - 3x + 3\), phương trình (*) trở thành \(f'\left( t \right) = \dfrac{1}{2}\left( {t + 1} \right)\), do đó số nghiệm của phương trình là số giao điểm của đồ thị hàm số \(y = f'\left( t \right)\) và \(y = \dfrac{1}{2}\left( {t + 1} \right)\).

Dựa vào đồ thị hàm số ta thấy \(\left( * \right) \Leftrightarrow \left[ \begin{array}{l}t =  - 1\\t = 1\\t = 5\\t=t_0\in (1;5)\end{array} \right.\)

+ Với \(t =  - 1 \Rightarrow {x^3} - 3x + 3 =  - 1\), phương trình này có 1 nghiệm không nguyên.

+ Với \(t = 1 \Rightarrow {x^3} - 3x + 3 = 1 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x =  - 2\end{array} \right.\), trong đó \(x = 1\) là nghiệm bội 2.

+ Với \(t = 5 \Rightarrow {x^3} - 3x + 3 = 5 \Leftrightarrow \left[ \begin{array}{l}x = 2\\x =  - 1\end{array} \right.\), trong đó \(x =  - 1\) là nghiệm bội 2.

+ Với \(t = {t_0} \in \left( {1;5} \right) \Rightarrow 1 < {t_0} < 5\) ta có phương trình \({x^3} - 3x + 3 = {t_0}\)

Xét hàm số \(h\left( x \right) = {x^3} - 3x + 3\) ta có:

\(h'\left( x \right) = 3{x^2} - 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x =  - 1\end{array} \right.\)

BBT:

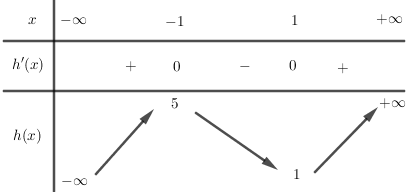
Từ BBT suy ra phương trình \({x^3} - 3x + 3 = {t_0}\) có \(3\) nghiệm phân biệt.

Suy ra phương trình \(g'\left( x \right) = 0\) có 8 nghiệm phân biệt và \(g'\left( x \right)\) đổi dấu qua các nghiệm này (\(x =  \pm 1\) là nghiệm bội ba) nên hàm số \(g\left( x \right)\) có 8 điểm cực trị.