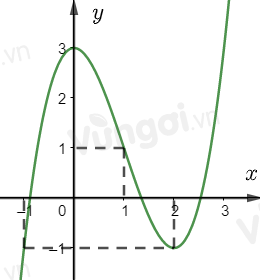
Cho hàm số y=f(x) có đồ thị như hình vẽ sau:
Số nghiệm của phương trình [f(x2+1)]2−2f(x2+1)−3=0 là
Chỉ được phép điền số 0, nguyên âm, nguyên dương và phân số dạng a/b
Đáp án:
Trả lời bởi giáo viên
Đáp án:
Đặt t=x2+1⇒t≥1
Ta thấy ứng với t = 1 cho ta một giá trị của x và ứng với mỗi giá trị t > 1 cho ta hai giá trị của x.
Phương trình đã cho trở thành: [f(t)]2−2f(t)−3=0⇔[f(t)=−1f(t)=3
Từ đồ thị hàm số y=f(t) trên [1;+∞) suy ra
+) Phương trình f(t)=−1 có 1 nghiệm t=2
=> [f(x2+1)]2−2f(x2+1)−3=0 có 2 nghiệm.
+) Phương trình f(t)=3 có 1 nghiệm t>2
=> [f(x2+1)]2−2f(x2+1)−3=0 có 2 nghiệm.
Vậy phương trình đã cho có 4 nghiệm.
Hướng dẫn giải:
- Đặt t=x2+1⇒t≥1
- Ứng với t = 1 cho ta một giá trị của x và ứng với mỗi giá trị t > 1 cho ta hai giá trị của x.
- Tìm số nghiệm của các phương trình f(t)=m rồi tìm x.


