Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên:
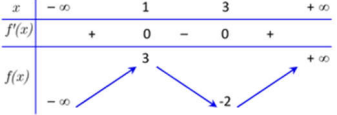
Số điểm cực đại của hàm số \(y = f\left( {3 - {x^2}} \right)\) là
Trả lời bởi giáo viên
Đặt \(g\left( x \right) = f\left( {3 - {x^2}} \right)\)
Ta có: \(g'\left( x \right) = \left[ {f\left( {3 - {x^2}} \right)} \right]'\)\( = \left( {3 - {x^2}} \right)'.f'\left( {3 - {x^2}} \right)\)\( = - 2x.f'\left( {3 - {x^2}} \right)\)
\(\begin{array}{l}g'\left( x \right) = 0 \Leftrightarrow - 2x.f'\left( {3 - {x^2}} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\\f'\left( {3 - {x^2}} \right) = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\3 - {x^2} = 1\\3 - {x^2} = 3\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \sqrt 2 \\x = - \sqrt 2 \end{array} \right.\end{array}\)
Các nghiệm trên đều là nghiệm bội lẻ.
Bảng biến thiên:
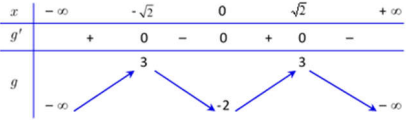
Chọn \(x = 1 \in \left( {0;\sqrt 2 } \right) \Rightarrow g'\left( 1 \right) = - 2.f'\left( 2 \right) > 0\) (Vì \(f'\left( 2 \right) < 0\))
Từ bảng biến thiên ta thấy hàm số có 2 điểm cực đại.
Hướng dẫn giải:
- Đặt \(g\left( x \right) = f\left( {3 - {x^2}} \right)\)
- Tính $g’(x)$ và giải \(g'\left( x \right) = 0\)
- Lập bảng xét dấu g’(x)


