Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:

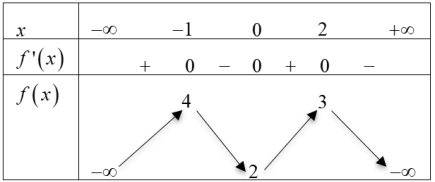
Bất phương trình \(\left( {{x^2} + 1} \right)f\left( x \right) \ge m\) có nghiệm thuộc khoảng \(\left( { - 1;2} \right)\) khi nào?

Đặt \(g\left( x \right) = \left( {{x^2} + 1} \right)f\left( x \right)\)

Bất phương trình \(\left( {{x^2} + 1} \right)f\left( x \right) \ge m\) có nghiệm thuộc khoảng \(\left( { - 1;2} \right)\) khi và chỉ khi:

\(m < \mathop {\max }\limits_{\left[ { - 1;2} \right]} g\left( x \right)\)

Ta có: \(g'\left( x \right) = 2x.f\left( x \right) + \left( {{x^2} + 1} \right).f'\left( x \right)\)

Từ bảng biến thiên ta sẽ thấy \(f'\left( 0 \right) = 0\)

\( \Rightarrow g'\left( 0 \right) = 0\)

Xét \(x \in \left( { - 1;0} \right)\)\( \Rightarrow \left\{ \begin{array}{l}2x.f\left( x \right) < 0\\\left( {{x^2} + 1} \right).f'\left( x \right) < 0\end{array} \right. \Rightarrow g'\left( x \right) < 0\)

Xét \(x \in \left( {1;2} \right)\)\( \Rightarrow \left\{ \begin{array}{l}2x.f\left( x \right) > 0\\\left( {{x^2} + 1} \right)f'\left( x \right) > 0\end{array} \right. \Rightarrow g'\left( x \right) > 0\)

\(g\left( 0 \right) = f\left( 0 \right) = 2\); \(g\left( { - 1} \right) = 2f\left( { - 1} \right) = 8;\)\(g\left( 2 \right) = 5.f\left( 2 \right) = 15\)

Ta có bảng biến thiên của hàm số \(y = g\left( x \right)\) trên \(\left[ { - 1;2} \right]\)

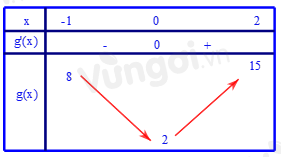
Từ bảng biến thiên ta thấy \(\mathop {\max }\limits_{\left[ { - 1;2} \right]} g\left( x \right) = 15 \Leftrightarrow x = 2\)

Vậy m<15