Câu hỏi:
3 năm trước
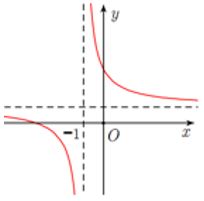
Cho hàm số \(y = \dfrac{{ax + b}}{{x + 1}}\) có đồ thị như hình vẽ bên. Tìm khẳng định đúng trong các khẳng định sau:
Trả lời bởi giáo viên
Đáp án đúng: d
Đồ thị hàm số có đường tiệm cận ngang \(y = a\). Theo hình vẽ, ta có: \(a > 0.\)
Đồ thị hàm số cắt trục hoành tại điểm \(A\left( { - \dfrac{b}{a};0} \right)\)
Theo hình vẽ, ta có: \( - \dfrac{b}{a} < - 1 \Leftrightarrow \dfrac{b}{a} > 1 \Rightarrow \dfrac{{b - a}}{a} > 0\).
Mà \(a > 0 \Rightarrow b - a > 0 \Leftrightarrow b > a\)
Vậy \(b > a > 0\).
Hướng dẫn giải:
Dựa vào TCN của đồ thị hàm số và giao điểm của đồ thị hàm số với trục hoành.

