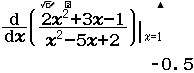Câu hỏi:
2 năm trước
Cho hàm số \(y = \dfrac{{2{x^2} + 3x - 1}}{{{x^2} - 5x + 2}}\). Đạo hàm y’ của hàm số là:
Trả lời bởi giáo viên
Đáp án đúng: d
\(\begin{array}{l}y' = \dfrac{{\left( {2{x^2} + 3x - 1} \right)'\left( {{x^2} - 5x + 2} \right) - \left( {2{x^2} + 3x - 1} \right)\left( {{x^2} - 5x + 2} \right)'}}{{{{\left( {{x^2} - 5x + 2} \right)}^2}}}\\y' = \dfrac{{\left( {4x + 3} \right)\left( {{x^2} - 5x + 2} \right) - \left( {2{x^2} + 3x - 1} \right)\left( {2x - 5} \right)}}{{{{\left( {{x^2} - 5x + 2} \right)}^2}}}\\y' = \dfrac{{4{x^3} - 20{x^2} + 8x + 3{x^2} - 15x + 6 - 4{x^3} - 6{x^2} + 2x + 10{x^2} + 15x - 5}}{{{{\left( {{x^2} - 5x + 2} \right)}^2}}}\\y' = \dfrac{{ - 13{x^2} + 10x + 1}}{{{{\left( {{x^2} - 5x + 2} \right)}^2}}}\end{array}\)
Hướng dẫn giải:
Sử dụng công thức tính đạo hàm của một thương \(\left( {\dfrac{u}{v}} \right)' = \dfrac{{u'v - uv'}}{{{v^2}}}\)
Giải thích thêm:
Có thể bấm máy tính để chọn được đáp án nhanh hơn như sau:
Bấm SHIFT d/dx rồi nhập vào hàm số đã cho, cho x=1 rồi ấn = sẽ ra kết quả -0,5.
Lần lượt thay x=1 vào từng đáp án sẽ thấy chỉ có đáp án D ra kết quả -0,5 nên chọn D.
