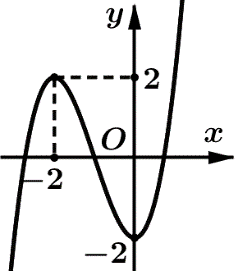
Cho hàm số \(f\left( x \right) = a{x^3} + b{x^2} + cx + d\) (với \(a,\)\(b,\)\(c,\)\(d \in \mathbb{R}\) và \(a \ne 0\)) có đồ thị như hình vẽ. Số điểm cực trị của hàm số \(g\left( x \right) = f\left( { - 2{x^2} + 4x} \right)\) là

Cho hàm số $y = f\left( x \right)$ có đạo hàm trên $\left( {a;b} \right)$. Nếu $f'\left( x \right)$ đổi dấu từ âm sang dương qua điểm ${x_0}$ thuộc \((a;b)\) thì

Giả sử $y = f\left( x \right)$ có đạo hàm cấp hai trên $\left( {a;b} \right)$. Nếu $\left\{ \begin{gathered}f'\left( {{x_0}} \right) = 0 \hfill \\ f''\left( {{x_0}} \right) > 0 \hfill \\ \end{gathered}  \right.$ thì 

Nếu ${x_0}$ là điểm cực tiểu của hàm số thì $f\left( {{x_0}} \right)$ là:

Nếu ${x_0}$ là điểm cực đại của hàm số thì $\left( {{x_0};f\left( {{x_0}} \right)} \right)$ là:

Đề chính thức ĐGNL HCM 2021

Khoảng cách giữa 2 điểm cực trị của hàm số \(y =  - {x^3} + 3x + 2\) là

Cho các phát biểu sau:

1. Hàm số $y = f\left( x \right)$ đạt cực đại tại ${x_0}$ khi và chỉ khi đạo hàm đổi dấu từ dương sang âm qua ${x_0}$.

2. Hàm số $y = f\left( x \right)$ đạt cực trị tại ${x_0}$ khi và chỉ khi ${x_0}$ là nghiệm của đạo hàm.

3. Nếu $f'\left( {{x_0}} \right) = 0$ và $f''\left( {{x_0}} \right) = 0$ thì ${x_0}$ không phải là cực trị của hàm số $y = f\left( x \right)$ đã cho.

4. Nếu $f'\left( {{x_0}} \right) = 0$ và $f''\left( {{x_o}} \right) > 0$ thì hàm số đạt cực đại tại ${x_0}$.

Các phát biểu đúng là:

Điều kiện để hàm số bậc ba không có cực trị là phương trình $y' = 0$ có: