Cho hàm số \(f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và có đồ thị của hàm số \(y = f'\left( x \right)\) như hình vẽ

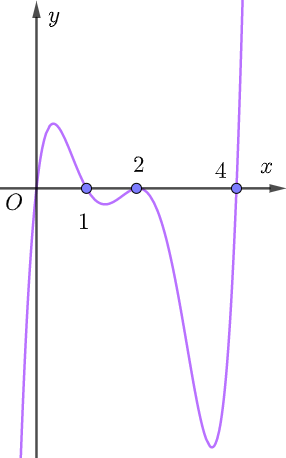
Số điểm cực trị của hàm số \(y = g\left( x \right) = f\left( {x - 2020} \right) - 2021x + 2022\) là

Chỉ được điền các số nguyên, phân số dạng a/b

Đáp án:

Biểu đồ dưới đây biểu thị tần suất về cân nặng của 35 học sinh.

Lớp giá trị [52;57] có tần số là:

Cho phương trình: $2 x^{2}+(2 m-1) x+m-1=0$. Tìm $m$ để phương trình có 2 nghiệm âm.

Cho hai đường tròn \(\left( {{C_1}} \right):{x^2} + {y^2} - 2y - 8 = 0\) và \(\left( {{C_2}} \right):{x^2} + {y^2} - 2x + 2y - 2 = 0\). Trong các mệnh đề sau, mệnh đề nào đúng?

Cho tứ diện \({\rm{ABCD}}\). Điểm \({\rm{M}}\) thuộc đoạn \({\rm{AC}}\) ( \({\rm{M}}\) khác \({\rm{A}},{\rm{M}}\) khác \({\rm{C}}\) ). Mặt phẳng \((\alpha )\) đi qua \({\rm{M}}\) song song với \({\rm{AB}}\) và \({\rm{AD}}\). Thiết diện của \((\alpha )\) với tứ diện \({\rm{ABCD}}\) là hình gì?

Hình chóp $S . A B C$ có đáy $A B C$ là tam giác vuông tại \(A,BC = 2a,ABC = {60^\circ }\). Gọi \(M\) là trung điểm cạnh \({\rm{BC}}\) và \({\rm{SA}} = {\rm{SC}} = {\rm{SM}} = {\rm{a}}\sqrt 5 \). Khoảng cách từ \({\rm{S}}\) đến cạnh \({\rm{AB}}\) là:

Cho hình chóp $S . A B C D$ có đáy $A B C D$ là hình vuông cạnh $a, S A$ vuông góc với \((ABCD)\) cà \(SA = a\sqrt 6 \). Tính sin của góc tạo bởi $A C$ và mặt phẳng \((SBC)\).