Câu hỏi:
2 năm trước
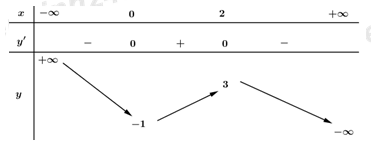
Cho hàm số bậc ba $y = f\left( x \right)$ có đồ thị như hình vẽ
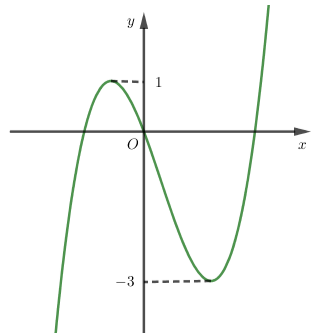
Tìm tất cả các giá trị của $m\;$ để hàm số $y = \left| {f\left( x \right) + m} \right|$ có ba điểm cực trị.
Trả lời bởi giáo viên
Đáp án đúng: a
Đồ thị hàm số $y = f\left( x \right) + m$ có được bằng cách tịnh tiến đồ thị hàm số $y = f\left( x \right)$ theo phương của trục $Oy$ $m$ đơn vị (lên trên hay xuống dưới phụ thuộc vào \(m\) dương hay âm), do đó nó đồ thị hàm số $y = f\left( x \right) + m$ có ${y_{CD}} = 1 + m;{\mkern 1mu} {\mkern 1mu} {y_{CT}} = - 3 + m$
Lấy đối xứng phần dưới của đồ thị hàm số \(y = f\left( x \right) + m\) qua \(Ox\) ta được đồ thị hàm số \(y = \left| {f\left( x \right) + m} \right|\)
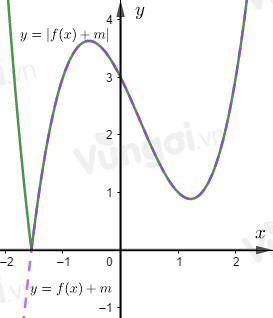
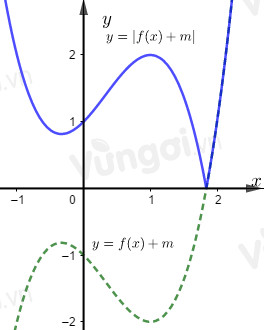
Để đồ thị hàm số $y = \left| {f\left( x \right) + m} \right|$ có ba điểm cực trị thì đồ thị hàm số \(y=f\left( x \right) + m\) cắt trục \(Ox\) tại đúng một điểm tức là điểm cực tiểu nằm trên trục \(Ox\) hoặc điểm cực đại nằm dưới trục \(Ox\), hay:
$\left[ {\begin{array}{*{20}{l}}{{y_{CT}} = {\rm{\;}} - 3 + m \ge 0}\\{{y_{CD}} = 1 + m \le 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m \ge 3}\\{m \le {\rm{\;}} - 1}\end{array}} \right.$
Hướng dẫn giải:
+) Dựa vào đồ thị hàm số $y = f\left( x \right)$ suy ra các giá trị cực trị của đồ thị hàm số $y = f\left( x \right) + m$ và dựa vào cách vẽ đồ thị hàm số $y = \left| {f\left( x \right) + m} \right|$.
+) Số điểm cực trị của hàm số $y = \left| {f\left( x \right) + m} \right|$. Bằng số điểm cực trị của hàm số $y = f\left( x \right) + m$ cộng với số giao điểm của đồ thị $y = f\left( x \right) + m$ và trục \(Ox\).
Câu hỏi khác
- Đề thi thử THPTQG môn Toán Chuyên ĐH Vinh Nghệ An lần 3 Toán 12 có lời giải chi tiết
- Đề thi thử THPTQG - Đề số 2 Toán 12 có lời giải chi tiết
- Đề thi thử THPTQG - Đề số 1 Toán 12 có lời giải chi tiết
- Đề tập huấn thi THPTQG Sở Giáo Dục và Đào Tạo Bắc Ninh 2019 Toán 12 có lời giải chi tiết
- Đề thi thử THPTQG - Đề số 4 Toán 12 có lời giải chi tiết
