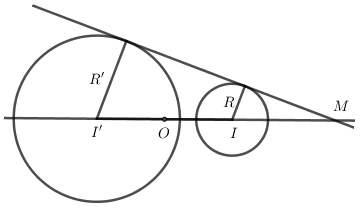
Cho hai tròn ngoài nhau \(\left( {I;R} \right)\) và \(\left( {I';R'} \right)\) với \(R \ne R'\) . Khẳng định nào sau đây là sai ?
Trả lời bởi giáo viên
Đáp án A: Gọi $M$ là giao điểm của của đường thẳng nối tâm với tiếp tuyến chung ngoài.
Ta có: \(\left\{ \begin{array}{l}\overrightarrow {MI'} = \overrightarrow {MI} .\dfrac{{MI'}}{{MI}} = \overrightarrow {MI} .\dfrac{{R'}}{R} = k\overrightarrow {MI} \\R' = \left| k \right|.R\end{array} \right.\)
\( \Rightarrow {V_{\left( {M;\frac{{R'}}{R}} \right)}}\) biến đường tròn \(\left( {I;R} \right)\) thành \(\left( {I';R'} \right)\)
\( \Rightarrow \) Đáp án A đúng.
Hiển nhiên đáp án B đúng.
Đáp án C: Giả sử phép vị tự tâm $M$ tỉ số k biến \(\left( {I;R} \right)\) thành \(\left( {I';R'} \right)\)\( \Rightarrow \left| k \right| = \dfrac{{R'}}{R} \Rightarrow \left[ \begin{array}{l}k = \dfrac{{R'}}{R}\\k = - \dfrac{{R'}}{R}\end{array} \right.\)
\( \Rightarrow \) Có hai tâm vị tự biến \(\left( {I;R} \right)\) thành \(\left( {I';R'} \right)\)
\( \Rightarrow C\) đúng.
Đáp án D: Gọi $O$ là trung điểm của $II'$, giả sử phép vị tự tâm $O$ tỉ số $k$ biến \(\left( {I;R} \right)\) thành \(\left( {I';R'} \right)\)
\(\begin{array}{l} \Rightarrow \overrightarrow {OI'} = k\overrightarrow {OI} \Rightarrow k = - 1\\ \Rightarrow R' = \left| { - 1} \right|R = R\,\,\left( {ktm} \right)\end{array}\)
\( \Rightarrow \) Đáp án D sai.