Cho \(f\left( x \right)\) là hàm số đa thức bậc ba có bảng biến thiên:
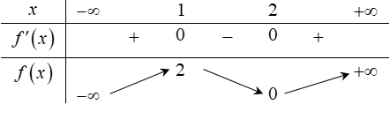
Số điểm cực trị của hàm số \(f\left( {\sqrt {3 + 2x - {x^2}} } \right)\) là
Trả lời bởi giáo viên
Ta có: \(D = \left[ { - 1;3} \right]\)
Đặt \(t = \sqrt {3 + 2x - {x^2}} \)
\(t' = \dfrac{{1 - x}}{{\sqrt {3 + 2x - {x^2}} }}\)
\(t' = 0 \Leftrightarrow 1 - x = 0 \Leftrightarrow x = 1\)
Bảng biến thiên của hàm số \(t = t\left( x \right)\):
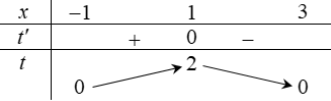
Thay x thành t và thu được bảng biến thiên:
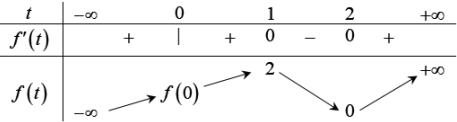
Từ hai bảng biến thiên trên ta lập luận và suy ra bảng biến thiên của hàm số \(f\left( {\sqrt {3 + 2x - {x^2}} } \right)\) trên đoạn \(\left[ { - 1;3} \right]\)
Khi x tăng từ -1 đến 1 thì t tăng từ 0 đến 2.
Khi đó \(f\left( t \right)\) tăng từ \(f\left( 0 \right)\) lên 2 rồi giảm xuống 0.
Khi x tăng từ 1 đến 3 thì t giảm từ 2 đến 0.
Khi đó \(f\left( t \right)\) tăng từ 0 lên 2 rồi giảm xuống \(f\left( 0 \right)\).
Vậy hàm số \(f\left( {\sqrt {3 + 2x - {x^2}} } \right)\) có 3 điểm cực trị.
Hướng dẫn giải:
- Đặt \(t = \sqrt {3 + 2x - {x^2}} \)
- Khảo sát hàm số \(t = t\left( x \right)\)
- Thay x thành t và lập bảng biến thiên
- Suy ra bảng biến thiên của hàm số \(f\left( {\sqrt {3 + 2x - {x^2}} } \right)\) trên đoạn \(\left[ { - 1;3} \right]\)
- Tìm số điểm cực trị
Câu hỏi khác
- Đề thi ĐGNL Hà Nội - Đề số 1 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 2 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 10 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 7 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 9 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
