Cho đường tròn $(O)$ đường kính $AB$ và một cung $AC$ có số đo nhỏ hơn $90^\circ $. Vẽ dây $CD$ vuông góc với $AB$ và dây $DE$ song song với $AB$. Chọn kết luận sai?
Trả lời bởi giáo viên
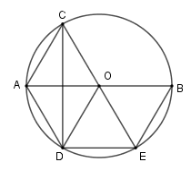
Vì $AO \bot CD;AO{\rm{//}}DE \Rightarrow CD \bot DE$$ \Rightarrow \widehat {CDE} = 90^\circ $ mà $C,D,E \in \left( O \right)$ nên $CE$ là đường kính hay $C;O;E$ thẳng hàng
Xét $\left( O \right)$ có $OA$ là đường cao trong tam giác cân $ODC$ nên $OA$ cũng là đường phân giác $ \Rightarrow \widehat {COA} = \widehat {AOD}$
Suy ra cung $AD$ bằng cung $AC$ nên dây $AD = AC$
Lại thấy $\widehat {AOC} = \widehat {BOE}$ (đối đỉnh) nên cung $AC$ bằng cung $BE$ suy ra dây $AC = BE$.
Phương án A, B, C đúng.
Hướng dẫn giải:
Sử dụng liên hệ giữa dây và đường kính để so sánh các góc ở tâm từ đó so sánh các cung và dây cung

