Cho đường tròn $\left( O \right)$ có hai dây $AB,CD$ song song với nhau. Kết luận nào sau đây là đúng?
Trả lời bởi giáo viên
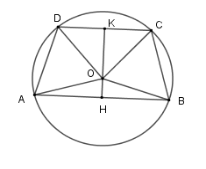
Kẻ $KH \bot CD$ và $KH \bot AB$ lần lượt tại $K$ và $H$.
Suy ra $OK$ vừa là đường cao, vừa là đường phân giác của $\widehat {DOC}$$ \Rightarrow \widehat {DOK} = \widehat {COK}$
Và $OH$ vừa là đường cao, vừa là đường phân giác của $\widehat {AOB}$$ \Rightarrow \widehat {AOH} = \widehat {BOH}$
Do đó $\widehat {AOH} + \widehat {DOK} = \widehat {BOH} + \widehat {COK} \Rightarrow \widehat {AOD} = \widehat {COB}$
Nên số đo cung $AD$ bằng số đo cung $BC$, từ đó $AD = BC$.
Phương án A, C, D sai và B đúng.
Hướng dẫn giải:
Sử dụng liên hệ giữa dây và đường kính để so sánh các góc ở tâm từ đó so sánh các cung và dây cung.
Giải thích thêm:
Lời giải trên chính là một cách chứng minh cho tính chất “Trong một đường tròn, hai cung bị chắn giữa hai dây song song thì bằng nhau.”

