Cho đường thẳng xy và đường tròn (O; R) không giao nhau. Gọi M là một điểm di động trên xy. Vẽ đường tròn đường kính OM cắt đường tròn (O) tại A và B. Kẻ \(OH \bot xy\) . Chọn câu đúng.
Trả lời bởi giáo viên
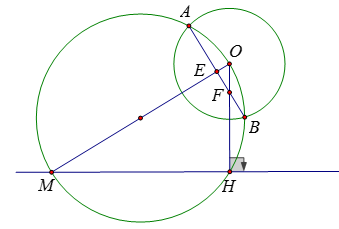
Vì \(OH \bot xy,\) nên \(H\) là một điểm cố định và \(OH\) không đổi
Gọi giao điểm của \(AB\) và \(OM\) là \(E;\) giao điểm của \(AB\) với \(OH\) là \(F.\)
Vì \(\left( {O;R} \right)\) và đường tròn đường kính \(OM\) cắt nhau tại \(A;B\) nên \(AB \bot OM\)
Lại có điểm A nằm trên đường tròn đường kính OM nên \(\widehat {OAM} = 90^\circ \)
Xét \(\Delta OEF\) và \(\Delta OHM\) có \(\widehat O\) chung và \(\widehat {OEF} = \widehat {OHM} = 90^\circ \) nên \(\Delta OEF \backsim \Delta OHM\left( {g - g} \right)\)
Suy ra \(\dfrac{{OE}}{{OH}} = \dfrac{{OF}}{{OM}} \Rightarrow OE.OM = OF.OH\)
Xét \(\Delta MAO\) vuông tại \(A\) có \(AE\) là đường cao nên theo hệ thức lượng trong tam giác vuông ta có
\(\begin{array}{*{20}{l}}{OM.OE = O{A^2}\; = {R^2}}\\{\; \Rightarrow OF.OH = {R^2}\; \Rightarrow OF = \dfrac{{{R^2}}}{{OH}}}\end{array}\)
Do \(OH\) không đổi nên \(OF\) cũng không đổi
Vậy \(F\) là một điểm cố định hay \(AB\) luôn đi qua một điểm cố định là giao của \(AB\) và \(OH.\)
Hướng dẫn giải:
+ Sử dụng tam giác đồng dạng
+ Sử dụng hệ thức lượng trong tam giác vuông để chỉ ra các điểm và đoạn thẳng cố định.

