Câu hỏi:
2 năm trước
Cho đường thẳng Δ và điểm O sao cho khoảng cách từ O đến Δ là OH = 1.

Với mỗi điểm M di động trong mặt phẳng, gọi K là hình chiếu vuông góc của M lên Δ. Tập hợp các điểm M trong mặt phẳng sao cho \(M{K^2}--M{O^2}\; = 1\) là một đường:
Trả lời bởi giáo viên
Đáp án đúng:
A.parabol
Chọn hệ trục toạ độ sao cho điểm O trùng với gốc toạ độ và trục Ox trùng với đường thẳng OH.
Giả sử M có toạ độ (x; y) thì K có toạ độ là (–1; y).
Khi đó:
\(M{K^2}-M{O^2}\; = 1\)
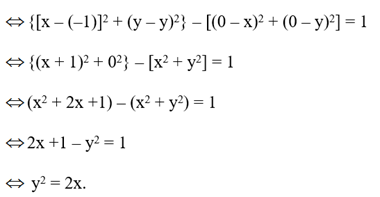
Vậy tập hợp các điểm M là parabol có phương trình \({y^2}\; = 2x.\)
Hướng dẫn giải:
Chọn hệ trục toạ độ sao cho điểm O trùng với gốc toạ độ và trục Ox trùng với đường thẳng OH.
Giả sử M có toạ độ (x; y) thì K có toạ độ là (–1; y).
Thay độ dài MK và MO vào: \(M{K^2}-M{O^2}\; = 1\)


