Câu hỏi:
2 năm trước
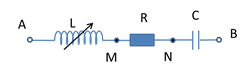
Cho đoạn mạch AB gồm điện trở thuần R, cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C mắc nối tiếp; trong đó R và C không đổi, còn L thay đổi được. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều \(u = U\sqrt 2 {\rm{cos(}}\omega {\rm{t + }}{\varphi _u})\) (với \(U,\omega \) không đổi). Điều chỉnh L tới giá trị L1 thì hiệu điện thế hiệu dụng hai đầu cuộn cảm đạt giá trị cực đại và bằng ULmax. Gọi UCmax là giá trị hiệu điện thế hiệu dụng cực đại ở hai đầu tụ điện. Cho biết \({U_{L\max }} = \sqrt 5 {U_{Rm{\rm{ax}}}}\) . Hệ thức nào sau đây là đúng?
Trả lời bởi giáo viên
Đáp án đúng: a
- L biến thiên để URmax, UCmax<=> cộng hưởng điện
Khi đó: \(\left\{ \begin{array}{l}{U_{{R_{{\rm{max}}}}}} = U\\{U_{{C_{{\rm{max}}}}}} = \frac{U}{R}{Z_C}\end{array} \right.\)
- L biến thiên để ULmax
Khi đó: \({U_{{L_{{\rm{max}}}}}} = \dfrac{{U\sqrt {{R^2} + Z_C^2} }}{R}\)
Theo đề bài, ta có:
\(\begin{array}{l}{U_{{L_{{\rm{max}}}}}} = \sqrt 5 {U_{{R_{{\rm{max}}}}}} = \sqrt 5 U\\ \to \dfrac{{U\sqrt {{R^2} + Z_C^2} }}{R} = \sqrt 5 U \to \sqrt {{R^2} + Z_C^2} = \sqrt 5 R\\ \to Z_C^2 = 4{R^2} \to {Z_C} = 2R\end{array}\)
=> Tỉ số: \(\dfrac{{{U_{{C_{{\rm{max}}}}}}}}{{{U_{{L_{{\rm{max}}}}}}}} = \dfrac{{\dfrac{U}{R}{Z_C}}}{{\sqrt 5 U}} = \dfrac{{{Z_C}}}{{\sqrt 5 R}} = \dfrac{{2R}}{{\sqrt 5 R}} = \dfrac{2}{{\sqrt 5 }}\)
Câu hỏi khác
- Bài tập các mạch điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập mạch RLC mắc nối tiếp có lời giải MÔN LÝ lớp 12
- Bài tập pha u,i - viết phương trình u, i có lời giải MÔN LÝ lớp 12
- Bài tập lý thuyết đại cương về dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập đại cương dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
