Cho \(\Delta ABC\), lấy 2 điểm $D$ và $E$ lần lượt nằm bên cạnh $AB$ và $AC$ sao cho \(\dfrac{{AD}}{{AB}} = \dfrac{{AE}}{{AC}}\). Kết luận nào sai?
Trả lời bởi giáo viên
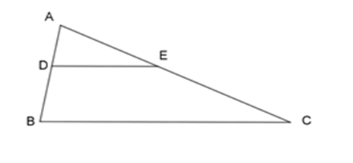
Xét $\Delta ADE$ và $\Delta ABC$ ta có:
\(\dfrac{{AD}}{{AB}} = \dfrac{{AE}}{{AC}}\) (theo gt)
$\widehat A$ chung.
$ \Rightarrow \Delta ADE\backsim\Delta ABC$ (c – g – c)
$ \Rightarrow \widehat {ADE} = \widehat {ABC}$ (cặp góc tương ứng)
$ \Rightarrow \dfrac{{AD}}{{AB}} = \dfrac{{AE}}{{AC}} = \dfrac{{DE}}{{BC}} \Rightarrow DE{\rm{//}}BC$ (định lý Talet đảo)
Hướng dẫn giải:
Bước 1: Chứng minh cặp tam giác đồng dạng theo trường hợp cạnh – góc – cạnh.
Bước 2: Áp dụng định lý Talet đảo để tìm ra nhận định sai.
Giải thích thêm:
- Học sinh cần viết các cặp đoạn thẳng tỉ lệ và cặp tam giác đồng dạng theo đúng thứ tự đỉnh tương ứng của 2 tam giác.