Câu hỏi:
2 năm trước
Cho \(\Delta ABC\) có $AB > AC$ . Kẻ $BN$ là tia phân giác của góc $B$ \(\left( {N \in AC} \right)\). Kẻ $CM$ là tia phân giác của góc $C$\(\left( {M \in AB} \right)\), $CM$ và $BN$ cắt nhau tại $I.$ So sánh $IC$ và $IB?$
Trả lời bởi giáo viên
Đáp án đúng: d
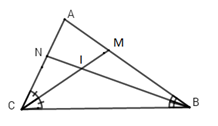
Vì \(AB > AC \Rightarrow \widehat {ACB} > \widehat {ABC}\left( 1 \right)\) (quan hệ giữa cạnh và góc trong tam giác)
Vì $BN$ là phân giác của \(\widehat {ABC} \Rightarrow \widehat {NBC} = \dfrac{{\widehat {ABC}}}{2}\left( 2 \right)\) (tính chất phân giác)
Vì $CM$ là phân giác của \(\widehat {ACB} \Rightarrow \widehat {MCB} = \dfrac{{\widehat {ACB}}}{2}\left( 3 \right)\) (tính chất phân giác)
Từ \(\left( 1 \right)\left( 2 \right)\left( 3 \right)\) \(\Rightarrow \widehat {MCB} > \widehat {NBC}\,\,hay\,\,\,\widehat {ICB} > \widehat {IBC}.\)
Xét \(\Delta BIC\) có \(\widehat {MCB} > \widehat {NBC}\left( {cmt} \right) \Rightarrow IB > IC\) (quan hệ giữa góc và cạnh trong tam giác)
Hướng dẫn giải:
- Áp dụng tính chất tia phân giác của một góc.
- Chứng minh \(\widehat {MCB} > \widehat {NBC}\) .
- Áp dụng định lý: Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.
