Câu hỏi:
2 năm trước
Cho \(\Delta ABC\) có \(\widehat A = {70^0}\), các đường phân giác $BE$ và $CD$ của \(\widehat B\) và \(\widehat C\) cắt nhau tại $I.$ Tính \(\widehat {BIC}\)?
Trả lời bởi giáo viên
Đáp án đúng: a
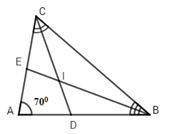
Xét \(\Delta ABC\) có: \(\widehat A + \widehat {ACB} + \widehat {ABC} = {180^0}\) (định lý tổng ba góc trong một tam giác)
\( \Rightarrow \widehat {ACB} + \widehat {ABC} = {180^0} - \widehat A = {180^0} - {70^0} = {110^0}\left( 1 \right)\)
Vì $CD$ là phân giác của \(\widehat {ACB}\left( {gt} \right) \Rightarrow \widehat {DCB} = \dfrac{{\widehat {ACB}}}{2}\left( 2 \right)\) (tính chất tia phân giác)
Vì $BE $ là phân giác của \(\widehat {ABC}\left( {gt} \right) \Rightarrow \widehat {CBE} = \dfrac{{\widehat {ABC}}}{2}\left( 3 \right)\) (tính chất tia phân giác)
Từ $(1), (2)$ và $(3)$ \( \Rightarrow \widehat {DCB} + \widehat {CBE} = \dfrac{{\widehat {ACB}}}{2} + \dfrac{{\widehat {ABC}}}{2} = \dfrac{{\widehat {ACB} + \widehat {ABC}}}{2} = {110^0}:2 = {55^0}\) hay \(\widehat {ICB} + \widehat {IBC} = {55^0}\left( * \right)\)
Xét \(\Delta BIC\) có: \(\widehat {ICB} + \widehat {IBC} + \widehat {BIC} = {180^0}\left( {**} \right)\)( định lý tổng ba góc trong một tam giác)
Từ (*) và (**) \( \Rightarrow \widehat {BIC} = {180^0} - \left( {\widehat {ICB} + \widehat {IBC}} \right) = {180^0} - {55^0} = {125^0}\)
Hướng dẫn giải:
Áp dụng định lý tổng ba góc trong một tam giác, tính chất tia phân giác của một góc.
Câu hỏi khác
- Đề kiểm tra 15 phút chương 7: quan hệ giữa các yếu tố trong tam giác. các đường đồng quy trong tam giác - đề số 2 Toán 7 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 7: quan hệ giữa các yếu tố trong tam giác. các đường đồng quy trong tam giác - đề số 1 Toán 7 có lời giải chi tiết
- Đề kiểm tra 45 phút chương 7: quan hệ giữa các yếu tố trong tam giác. các đường đồng quy trong tam giác - đề số 1 Toán 7 có lời giải chi tiết
- Đề kiểm tra 45 phút chương 7: quan hệ giữa các yếu tố trong tam giác. các đường đồng quy trong tam giác - đề số 2 Toán 7 có lời giải chi tiết
