Câu hỏi:
2 năm trước
Biểu thức \(\left( {4 - {x^2}} \right)\left( {{x^2} + 2x - 3} \right)\left( {{x^2} + 5x + 9} \right)\) âm khi
Trả lời bởi giáo viên
Đáp án đúng: d
Đặt \(f\left( x \right) = \left( {4 - {x^2}} \right)\left( {{x^2} + 2x - 3} \right)\left( {{x^2} + 5x + 9} \right)\)
Phương trình \(4 - {x^2} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = - 2\end{array} \right..\)
Phương trình \({x^2} + 2x - 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - \,3\end{array} \right..\)
Ta có \({x^2} + 5x + 9 = {\left( {x + \dfrac{5}{2}} \right)^2} + \dfrac{{11}}{4} > 0\)
Lập bảng xét dấu:
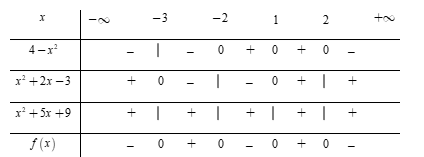
Dựa vào bảng xét dấu ta thấy \(\left( {4 - {x^2}} \right)\left( {{x^2} + 2x - 3} \right)\left( {{x^2} + 5x + 9} \right) < 0\) \( \Leftrightarrow \left[ \begin{array}{l}x < - 3\\ - 2 < x < 1\\x > 2\end{array} \right.\)
\( \Leftrightarrow x \in \left( { - \infty ; - 3} \right) \cup \left( { - 2;1} \right) \cup \left( {2; + \infty } \right).\)
Hướng dẫn giải:
Lập bảng xét dấu biểu thức và kết luận.
