Vật chịu tác dụng lực ngang F ngược chiều chuyển động thẳng trong $6s$. Vận tốc giảm từ $8m/s$ còn $5m/s$. Trong $10s$ tiếp theo lực tác dụng tăng gấp đôi về độ lớn còn hướng không đổi. Vận tốc của vật ở điểm cuối là:
Trả lời bởi giáo viên
Chọn chiều dương là chiều chuyển động của vật, ta có:
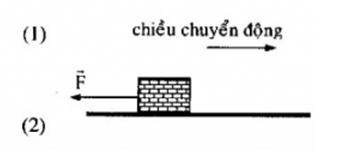
+ Trong $6s$ đầu: \({a_1} = \dfrac{{{v_1} - {v_{01}}}}{{{t_1}}} = \dfrac{{5 - 8}}{6} = - 0,5m/{s^2}\)
+ Trong $10s$ tiếp theo: \({a_2} = \frac{{{v_2} - {v_{02}}}}{{{t_2}}} = \dfrac{{{v_2} - 5}}{{10}}\) (1)
Ta có, với cùng một vật thì gia tốc a tỉ lệ thuận với lực tác dụng nên khi
\({F_2} = 2{F_1} \to {a_2} = 2{{\rm{a}}_1} = 2.( - 0,5) = - 1m/{s^2}\)
Thay vào (1) ta được: \(\dfrac{{{v_2} - 5}}{{10}} = - 1 \to {v_2} = - 5m/s\)
Hướng dẫn giải:
+ Vận dụng biểu thức xác định gia tốc: \(a = \frac{{\Delta v}}{{\Delta t}}\)
+ Vận dụng định luật II Niutơn: \(\overrightarrow F = m\overrightarrow a \)

