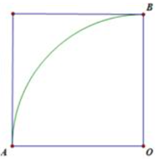
Từ một miếng tôn cạnh bằng \(8{\rm{dm}}\), người ta cắt ra một hình quạt tâm \({\rm{O}}\) bán kính \({\rm{OA}} = 8{\rm{dm}}\) (xem hình). Để cuộn lại thành một chiếc phễu hình nón (khi đó OA trùng với OB). Chiều cao chiếc phễu đó có số đo gần đúng (làm tròn đến 3 chữ số thập phân) là:

Cho bảng phân bố tần số ghép lớp thống kê độ dài của 70 lá dương xỉ trưởng thành

Số lá có độ dài dưới 30cm chiếm bao nhiêu phần trăm so

Cho phương trình $m x^{2}+2(m-2) x+m-3=0$. Xác định $m$ để phương trình có hai nghiệm trái dấu.

Trong mặt phẳng hệ trục $O x y$, cho điểm $E(2 ; 2)$ và các đường thẳng $d: x+y-2=0 ; \Delta: x+y-8=0$. Tìm tọa độ các điểm $F \in d$ và $K \in \Delta$ sao cho $\Delta E F K$ vuông cân tại E.

Cho bốn điểm $A, B, C, S$ không cùng ở trong một mặt phẳng. Gọi $I, H$ lần lượt là trung điểm của $S A, A B$. Trên $S C$ lấy điểm $K$ sao cho $I K$ không song song với $A C$ (K không trùng với các đầu mút). Gọi \(E\) là giao điểm của đường thẳng $B C$ với mặt phẳng $(I H K)$. Mệnh đề nào sau đây đúng?

Cho hình chóp S.ABCD có đáy là hình vuông, \({\rm{SA}}\) vuông góc với đáy, \({\rm{SA}} = {\rm{a}}\). Góc giữa đường thẳng \({\rm{SD}}\) và mặt phẳng \(({\rm{SAC}})\) bằng \({30^\circ }\). Tính khoảng cách từ điểm \({\rm{D}}\) đến mặt phẳng \(({\rm{SBM}})\) với \({\rm{M}}\) là trung điểm \({\rm{CD}}\).

Cho hình chóp $S . A B C$ có các và là các tam giác đều và nằm trong hai mặt phẳng vuông góc với nhau. Góc giữa đường thẳng $S A$ và \((ABC)\) bằng:

Hệ phương trình \(\left\{ \begin{align}  & 3\sqrt{4x+2y}-5\sqrt{2x-y}=2 \\ & 7\sqrt{4x+2y}+2\sqrt{2x-y}=32 \\\end{align} \right.\)có nghiệm là (x; y). Khi đó hiệu \(x-y=?\)