Cho bốn điểm $A, B, C, S$ không cùng ở trong một mặt phẳng. Gọi $I, H$ lần lượt là trung điểm của $S A, A B$. Trên $S C$ lấy điểm $K$ sao cho $I K$ không song song với $A C$ (K không trùng với các đầu mút). Gọi \(E\) là giao điểm của đường thẳng $B C$ với mặt phẳng $(I H K)$. Mệnh đề nào sau đây đúng?
Trả lời bởi giáo viên
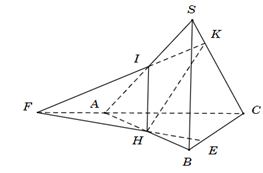
- Chọn mặt phẳng phụ $(A B C)$ chứa $B C$
Tìm giao tuyến của 2 mặt phẳng $(ABC)$ và $(IHK)$.
Ta có $H$ là điểm chung thứ nhất của $(A B C)$ và \((IHK)\).
Trong mặt phẳng \((SAC)\), do $I K$ không song song với $A C$ nên gọi \(F = IK \cap AC\). Ta có
- \(F \in AC\) mà \(AC \subset (ABC)\) suy ra \(F \in (ABC)\).
- \(F \in IK\) mà \(IK \subset (IHK)\) suy ra \(F \in (IHK)\).
Suy ra \(F\) là điểm chung thứ hai của \((ABC)\) và \((IHK)\).
Do đó \((ABC) \cap (IHK) = HF\).
- Trong mặt phẳng \((ABC)\), gọi \(E = HF \cap BC\). Ta có
- \(E \in HF\) mà \(HF \subset (IHK)\) suy ra \(E \in (IHK)\).
- \(E \in BC\).
Vậy \(E = BC \cap (IHK)\).
Hướng dẫn giải:
Chọn mặt phẳng phụ $(A B C)$ chứa $B C$
Tìm giao tuyến của 2 mặt phẳng \((ABC)\) và $(I H K)$.


