Câu hỏi:
2 năm trước
Cho hình chóp S.ABC có các và là các tam giác đều và nằm trong hai mặt phẳng vuông góc với nhau. Góc giữa đường thẳng SA và (ABC) bằng:
Trả lời bởi giáo viên
Đáp án đúng: a
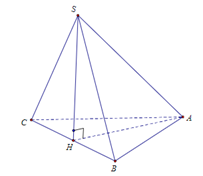
Theo giả thiết ta có (ABC)⊥(SBC).
Trong mặt phẳng (SBC) kẻ SH⊥BC⇒SH⊥(ABC) nên AH là hình chiếu của SA trên (ABC).
Do đó, (^SA,(ABC))=(^SA,AH)=^SAH.
Giả sử AB=a.
Ta có: và là tam giác đều nên H là trung điểm của BC và AH=SH=a√32.
Xét tam giác vuông SHA ta có tan^SAH=SHAH=1⇒^SAH=45∘.
Vậy (^SA,(ABC))=45∘.
Hướng dẫn giải:
Trong mặt phẳng (SBC) kẻ SH⊥BC⇒SH⊥(ABC) nên AH là hình chiếu của SA trên (ABC).
Từ đó xác định được góc giữa đường thẳng SA và (ABC) bằng:


