Cho hình chóp S.ABCD có đáy là hình vuông, \({\rm{SA}}\) vuông góc với đáy, \({\rm{SA}} = {\rm{a}}\). Góc giữa đường thẳng \({\rm{SD}}\) và mặt phẳng \(({\rm{SAC}})\) bằng \({30^\circ }\). Tính khoảng cách từ điểm \({\rm{D}}\) đến mặt phẳng \(({\rm{SBM}})\) với \({\rm{M}}\) là trung điểm \({\rm{CD}}\).

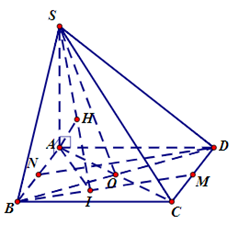
Chứng minh \({\rm{DB}} \bot ({\rm{SAC}}) \Rightarrow \) Hình chiếu vuông góc của \({\rm{DS}}\) lên \((SAC)\) là $S O$, góc giữa $S D$ và \((SAC)\) là \({\rm{DSO}} = {30^\circ }\).

Đặt \({\rm{DO}} = {\rm{x}}\), ta có \({\rm{SO}} = {\rm{x}}\sqrt 3 \) (O là giao của \({\rm{AC}}\) và \({\rm{BD}})\)

Từ \({\rm{S}}{{\rm{O}}^2} = {\rm{A}}{{\rm{O}}^2} + {\rm{S}}{{\rm{A}}^2} \Rightarrow {\rm{x}} = \dfrac{{\rm{a}}}{{\sqrt 2 }}\)

Gọi N là trung điểm của \({\rm{AB}} \Rightarrow {\rm{DN}}//{\rm{BM}}\)

Suy ra d \(({\rm{D}};({\rm{SBM}})) = {\rm{d}}({\rm{N}};({\rm{SBM}})) = \dfrac{1}{2}\;{\rm{d}}(\;{\rm{A}};({\rm{SBM}}))\)

Kẻ \({\rm{AI}} \bot {\rm{BM}},{\rm{AH}} \bot {\rm{SM}}\).

Từ đó chứng minh được \({\rm{AH}} \bot ({\rm{SBM}}) \Rightarrow {\rm{d}}({\rm{A}};({\rm{SBM}})) = {\rm{AH}}\)

Trong \((ABCD):{{\rm{S}}_{{\rm{ABM}}}} = {{\rm{S}}_{{\rm{ABCD}}}} - {{\rm{S}}_{{\rm{BCM}}}} = \dfrac{{{{\rm{a}}^2}}}{2}\)

Mà \({{\rm{S}}_{{\rm{ABM}}}} = \dfrac{1}{2}{\rm{AI}} \cdot {\rm{BM}} \Rightarrow {\rm{AI}} = \dfrac{{2{\rm{a}}}}{{\sqrt 5 }}\)

Khi đó: \(\dfrac{1}{{{\rm{A}}{{\rm{H}}^2}}} = \dfrac{1}{{{\rm{A}}{{\rm{I}}^2}}} + \dfrac{1}{{{\rm{S}}{{\rm{A}}^2}}} \Rightarrow {\rm{AH}} = \dfrac{2}{3}{\rm{a}} \Rightarrow {\rm{d}}({\rm{D}};({\rm{SBM}})) = \dfrac{{\rm{a}}}{3}\).