Câu hỏi:
2 năm trước
Trong mặt phẳng với hệ toạ độ $Oxy$, cho $2$ đường thẳng ${d_1}:x - 7y + 17 = 0,$
${d_2}:x + y - 5 = 0.$ Viết phương trình đường thẳng $d$ qua điểm $M\left( {0;1} \right)$ tạo với ${d_1},{d_2}$ một tam giác cân tại giao điểm của ${d_1},{d_2}$.
Trả lời bởi giáo viên
Đáp án đúng: a
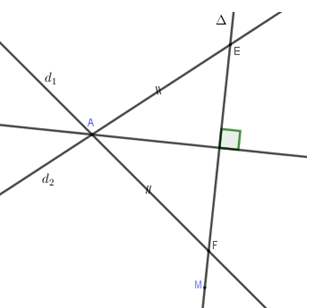
Phương trình đường phân giác góc tạo bởi ${d_1},{d_2}$ là:
$\dfrac{{\left| {x - 7y + 17} \right|}}{{\sqrt {{1^2} + {{( - 7)}^2}} }} = \dfrac{{\left| {x + y - 5} \right|}}{{\sqrt {{1^2} + {1^2}} }}$$ \Leftrightarrow \left[ \begin{array}{l}2x + 6y - 21 = 0{\rm{ (}}{\Delta _1}{\rm{)}}\\3x - y - 4 = 0{\rm{ (}}{\Delta _2}{\rm{)}}\end{array} \right.$
Đường thẳng cần tìm đi qua $M\left( {0;1} \right)$ và vuông góc với ${\Delta _1},{\Delta _2}$
+ Gọi \({d_3}\) là đường thẳng vuông góc với \({\Delta _1}\) thì \({d_3}\) có dạng: \(3x - y + c = 0\)
\({d_3}\) đi qua điểm \(M\left( {0;1} \right)\) nên \(3.0 - 1 + c = 0 \Leftrightarrow c = 1\) hay \(3x - y + 1 = 0\)
+ Gọi \({d_4}\) là đường thẳng vuông góc với \({\Delta _2}\) thì \({d_4}\) có dạng: \(x + 3y + c = 0\)
\({d_4}\) đi qua điểm \(M\left( {0;1} \right)\) nên \(0 + 3.1 + c = 0 \Leftrightarrow c = - 3\) hay \(x + 3y - 3 = 0\)
KL: $x + 3y - 3 = 0$ và $3x - y + 1 = 0$
Hướng dẫn giải:
- Viết phương trình đường phân giác của góc tạo bởi \({d_1}\) và \({d_2}\):
\(\dfrac{{{a_1}x + {b_1}y + {c_1}}}{{\sqrt {a_1^2 + b_1^2} }} = \pm \dfrac{{{a_2}x + {b_2}y + {c_2}}}{{\sqrt {a_2^2 + b_2^2} }}\)
- Đường thẳng cần tìm đi qua \(M\) và vuông góc với đường phân giác vừa viết.
