Tìm số nguyên m nhỏ nhất để bất phương trình \({\log _3}\left( {{x^2} + x + 1} \right) + 2{x^3}\)\( \le 3{x^2} + {\log _3}x + m - 1\) có ít nhất hai nghiệm phân biệt
Chỉ điền số nguyên, phân số dạng a/b
Đáp án:
Trả lời bởi giáo viên
Đáp án:
Ta có: \({\log _3}\left( {{x^2} + x + 1} \right) + 2{x^3}\)\( \le 3{x^2} + {\log _3}x + m - 1\)(1)
Điều kiện: x>0
\(\begin{array}{l}\left( 1 \right) \Leftrightarrow {\log _3}\left( {\dfrac{{{x^2} + x + 1}}{x}} \right) + 2{x^3} - 3{x^2} \le m - 1\\ \Leftrightarrow {\log _3}\left( {1 + x + \dfrac{1}{x}} \right) + 2{x^3} - 3{x^2} \le m - 1\end{array}\)
Xét \(f\left( x \right) = {\log _3}\left( {1 + x + \dfrac{1}{x}} \right) + 2{x^3} - 3{x^2}\) với x>0
\(\begin{array}{l}f'\left( x \right) = \dfrac{{1 - \dfrac{1}{{{x^2}}}}}{{\left( {1 + x + \dfrac{1}{x}} \right)\ln 3}} + 6{x^2} - 6x\\ = \dfrac{{{x^2} - 1}}{{{x^2}\left( {1 + x + \dfrac{1}{x}} \right)\ln 3}} + 6\left( {x - 1} \right)x\\f'\left( x \right) = 0 \Leftrightarrow x = 1\end{array}\)
Với \(x \in \left( {0;1} \right) \Rightarrow f'\left( x \right) < 0\)
Với \(x \in \left( {1; + \infty } \right) \Rightarrow f'\left( x \right) > 0\)
Ta có bảng biến thiên:
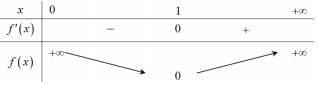
Vậy bất ohuowng trình có ít nhất hai nghiệm khi và chỉ khi \(m - 1 > 0 \Leftrightarrow m > 1\)
Vậy \(m = 2\)
Hướng dẫn giải:
- Tìm điều kiện
- Đưa bất phương trình về dạng \(f\left( x \right) = g\left( m \right)\)
- Xét \(f\left( x \right)\) với điều kiện đã tìm
- Tìm m


