Tìm m để phương trình \(\sqrt {{x^2} + x + 1}  - \sqrt {{x^2} - x + 1}  = m\) (1) có nghiệm

Xét hàm số \(y = f\left( x \right) = \sqrt {{x^2} + x + 1}  - \sqrt {{x^2} - x + 1} \)

\(D = \mathbb{R}\)

Ta có:

\(\begin{array}{l}y' = \dfrac{{2x + 1}}{{2\sqrt {{x^2} + x + 1} }} - \dfrac{{2x - 1}}{{2\sqrt {{x^2} - x + 1} }}\\y' = 0\\ \Leftrightarrow \dfrac{{2x + 1}}{{2\sqrt {{x^2} + x + 1} }} - \dfrac{{2x - 1}}{{2\sqrt {{x^2} - x + 1} }} = 0\\ \Leftrightarrow \left( {2x - 1} \right)\sqrt {{x^2} + x + 1}  = \left( {2x + 1} \right)\sqrt {{x^2} - x + 1} \\ \Leftrightarrow \left\{ \begin{array}{l}\left( {2x - 1} \right)\left( {2x + 1} \right) > 0\\{\left( {2x - 1} \right)^2}\left( {{x^2} + x + 1} \right) = {\left( {2x + 1} \right)^2}\left( {{x^2} - x + 1} \right)\end{array} \right.\end{array}\)

Ta thấy hệ trên vô nghiệm vì

\({\left( {2x - 1} \right)^2}\left( {{x^2} + x + 1} \right)\)\( = {\left( {2x + 1} \right)^2}\left( {{x^2} - x + 1} \right)\)

\( \Leftrightarrow {\left( {2x - 1} \right)^2}\left[ {{{\left( {2x + 1} \right)}^2} + 3} \right]\)\( = {\left( {2x + 1} \right)^2}\left[ {{{\left( {2x - 1} \right)}^2} + 3} \right]\)

\( \Leftrightarrow {\left( {2x - 1} \right)^2} = {\left( {2x + 1} \right)^2}\) \( \Leftrightarrow x = 0\) không thỏa mãn điều kiện.

Mà \(y'\left( 0 \right) = 1 > 0 \Rightarrow y' > 0\forall x\) nên hàm số đồng biến

\(\begin{array}{l}\mathop {\lim }\limits_{x \to  - \infty } y = \mathop {\lim }\limits_{x \to  - \infty } \dfrac{{2x}}{{\sqrt {{x^2} - x + 1}  + \sqrt {{x^2} + x + 1} }} =  - 1\\\mathop {\lim }\limits_{x \to  + \infty } y = \mathop {\lim }\limits_{x \to  + \infty } \dfrac{{2x}}{{\sqrt {{x^2} - x + 1}  + \sqrt {{x^2} + x + 1} }} = 1\end{array}\)

Từ đó ta có bảng biến thiên

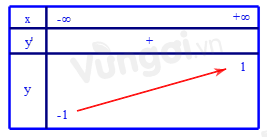
Phương trình có nghiệm khi và chỉ khi \( - 1 < m < 1\)