Trả lời bởi giáo viên
Ta có : (ab+ba)2=a2b2+2ab.ba+b2a2=a2b2+b2a2+2⇒a2b2+b2a2=(ab+ba)2−2
Biến đổi biểu thức P về dạng P=3(ab+ba)2−6−8(ab+ba)=3(ab+ba)2−8(ab+ba)−6
Đặt t=ab+ba⇒t2=(ab+ba)2.
Áp dụng bất đẳng thức (x+y)2≥4xy∀x,y với hai số ab và ba ta có : t2=(ab+ba)2≥4ab.ba=4⇔|t|≥2⇔[t≥2t≤−2
Biểu thức P trở thành P=3t2−8t−6.
Trục đối xứng x=−b2a=43 và hệ số a=3>0.
Suy ra hàm số f(t)=3t2−8t−6 nghịch biến trên khoảng (−∞;43) và đồng biến trên khoảng(43;+∞).
BBT :
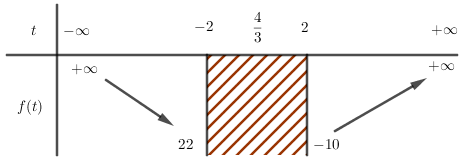
Từ đây suy ra hàm số f(t) đạt giá trị nhỏ nhất tại t=2
Ta có f(2)=−10.
Vậy min.
Hướng dẫn giải:
- Đặt t = \dfrac{a}{b} + \dfrac{b}{a} và tìm điều kiện cho t dựa theo bất đẳng thức {\left( {x + y} \right)^2} \ge 4xy.
- Biến đổi P = f\left( t \right) và tìm GTNN của f\left( t \right) với điều kiện của f\left( t \right) tìm được ở trên.
Giải thích thêm:
Một số em có thể sẽ xét nhầm hàm số trên khoảng [-2;2] dẫn đến chọn nhầm đáp án A là sai

