Câu hỏi:
1 năm trước
Tìm giá trị của m để hàm số \(y = - {x^2} + 2x + m - 5\) đạt giá trị lớn nhất bằng 6.
Đáp án: m=
Trả lời bởi giáo viên
Đáp án:
Đáp án: m=
Bước 1: Xác định hệ số $a$
Ta có $a=-1<0$
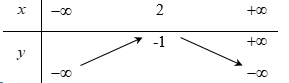
Hàm số đã cho đạt giá trị lớn nhất tại \(x = - {b \over {2a}} = 1\).
Bước 2: Tìm giá trị của hàm số tại $x=-\dfrac{b}{2a}$, tìm $m$.
Khi đó \(Maxy = f\left( 1 \right) = m - 4\).
Để \(Maxy = 6\) thì \(m - 4 = 6 \Leftrightarrow m = 10\).
Hướng dẫn giải:
Bước 1: Xác định hệ số $a$
Nếu $a<0$ thì hàm số $y=ax^2+bx+c$ đạt GTLN tại $x=-\dfrac{b}{2a}$
Bước 2: Tìm giá trị của hàm số tại $x=-\dfrac{b}{2a}$, tìm $m$.