Câu hỏi:
1 năm trước
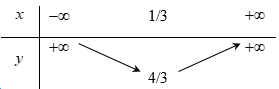
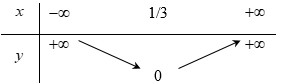
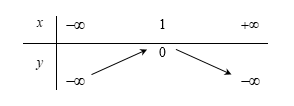
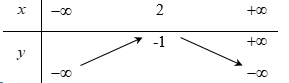
Parabol \(y = a{x^2} + bx + c\) đạt cực tiểu bằng 4 tại \(x = - 2\) và đi qua \(A\left( {0;6} \right)\) có phương trình là:
Đáp án: $y $
$x^2 $
$x $
Trả lời bởi giáo viên
Đáp án:
Đáp án: $y $
$x^2 $
$x $
Parabol \(y = a{x^2} + bx + c\) đạt cực đại bằng \(4\) khi \(x = - 2 \Rightarrow \) parabol có đỉnh \(I\left( { - 2;4} \right)\)
Lại có parabol đi qua điểm \(A\left( {0;6} \right)\) nên ta có: \(\left\{ {\begin{array}{*{20}{c}}{4a - 2b + c = 4}\\\begin{array}{l}c = 6\\ - \dfrac{b}{{2a}} = - 2\end{array}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = \dfrac{1}{2}}\\{b = 2}\\{c = 6}\end{array}} \right.} \right.\) .
Vậy parabol đã cho có hàm số: \(y = \dfrac{1}{2}{x^2} + 2x + 6.\)
Hướng dẫn giải:
Cho hàm số \(y = a{x^2} + bx + c{\rm{ }}\left( {a \ne 0} \right)\) có đồ thị \(\left( P \right)\)
Với \(a > 0:\) Giá trị nhỏ nhất của hàm số \({y_{\min }} = - \dfrac{\Delta }{{4a}}\) đạt được tại \(x = - \dfrac{b}{{2a}}.\)
\(\left( P \right)\) đi qua điểm \(A\left( {{x_0};{y_0}} \right) \Leftrightarrow {y_0} = a{x_0}^2 + b{x_0} + c.\)
