Một vật dao động điều hòa với phương trình \(x = 5cos\left( {4\pi t - \frac{\pi }{2}} \right)cm\). Xác định thời gian ngắn nhất để vật đi từ vị trí \(2,5cm\) đến \( - 2,5cm\)?
Trả lời bởi giáo viên
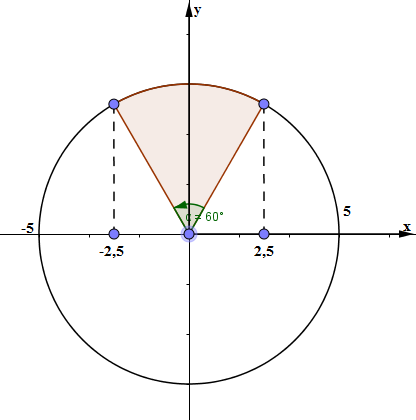
Từ đường tròn lượng giác ta thấy thời gian ngắn nhất khi vật đi từ vị trí 2,5 cm đến vị trí -2,5 cm quét được 1 góc \(\frac{\pi }{3}\) vậy áp dụng mối liên hệ gữa góc quét \(\alpha \) và khoảng thời gian \(\Delta t\) thì ta có:
\(\alpha = \frac{\pi }{3} = > \Delta t = \frac{\alpha }{\omega } = \frac{{\frac{\pi }{3}.T}}{{2\pi }} = \frac{T}{6}\)
Mà \(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{4\pi }} = \frac{1}{2}s = > \Delta t = \frac{{\frac{1}{2}}}{6} = \frac{1}{{12}}s\)
Hướng dẫn giải:
+ Ứng dụng đường tròn lượng giác và công thức \(\Delta t = \frac{\alpha }{\omega } = \frac{{\alpha .T}}{{2\pi }}\)
+ Sử dụng biểu thức tính chu kì: \(T = \frac{{2\pi }}{\omega }\)

