Câu hỏi:
1 năm trước
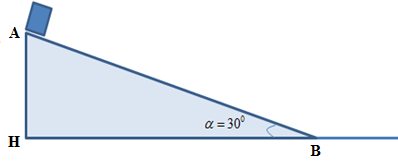
Một vật có khối lượng 600g trượt không tốc độ đầu từ đỉnh mặt phẳng nghiêng AB dài 3m, nghiêng 1 góc a = 300 so với mặt phẳng ngang. Cho g = 10m/s2. Chọn gốc thế năng tại chân mặt phẳng nghiêng. Bỏ qua ma sát tính cơ năng của vật ở đỉnh mặt phẳng nghiêng và tốc độ vật khi tới chân mặt phẳng nghiêng
Trả lời bởi giáo viên
Đáp án đúng: a
Vật chỉ chịu tác dụng của trọng lực nên cơ năng của vật được bảo toàn.
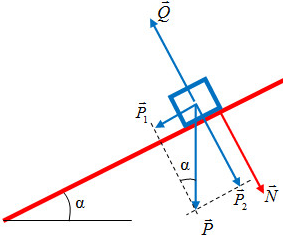
Chọn gốc thế năng tại chân mặt phẳng nghiêng
+ Xét tại A:
Cơ năng: \({{\rm{W}}_A} = {{\rm{W}}_{dA}} + {{\rm{W}}_{tA}} = \dfrac{1}{2}mv_A^2 + mg{z_A}\)
Với:
\(\begin{array}{l}\left\{ \begin{array}{l}{v_A} = 0\\{z_A} = AH = AB.\sin \alpha = 3.\sin 30 = 1,5m\end{array} \right.\\ \Rightarrow {{\rm{W}}_A} = 0,6.10.1,5 = 9J\end{array}\)
+ Xét tại B:
Cơ năng: \({{\rm{W}}_B} = {{\rm{W}}_{dB}} + {{\rm{W}}_{tB}} = \dfrac{1}{2}mv_B^2 + mg{z_B}\)
Với \({{\rm{z}}_B}{\rm{ = 0}} \Rightarrow {{\rm{W}}_B} = \dfrac{1}{2}mv_B^2 = 0,3.v_B^2\)
Có: \({{\rm{W}}_A}{\rm{ = }}{{\rm{W}}_B} \Leftrightarrow 0,3.v_B^2 = 9 \Rightarrow {v_B} = 5,48m/s\)
Hướng dẫn giải:
+ Cơ năng của vật chuyển động trong trọng trường : \({\rm{W}} = \dfrac{1}{2}.m.{v^2} + m.g.z\)
+ Áp dụng định luật bảo toàn cơ năng: \({{\rm{W}}_A} = {{\rm{W}}_B}\)
