Câu hỏi:
2 năm trước
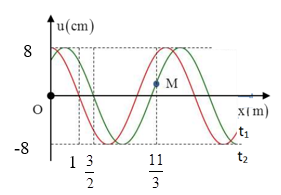
Một sóng hình sin đang truyền trên một sợi dây theo chiều dương của trục Ox. Hình vẽ mô tả hình dạng của sợi dây tại thời điểm \({t_1}\) và \({t_2} = {\rm{ }}{t_1} + {\rm{ }}1s\). Tại thời điểm \({t_2}\), vận tốc của điểm M trên dây gần giá trị nào nhất sau đây?
Trả lời bởi giáo viên
Đáp án đúng: b
Ta có: \(\dfrac{\lambda }{4} = 1 \to \lambda = 4m\)
Trong 1s sóng truyền đi được \(S = \dfrac{3}{2} - 1 = 0,5m \to v = \dfrac{S}{t} = \dfrac{{0,5}}{1} = 0,5m/s\)
Chu kì của sóng: \(T = \dfrac{\lambda }{v} = \dfrac{4}{{0,5}} = 8{\rm{s}} \to \omega = \dfrac{{2\pi }}{T} = \dfrac{\pi }{4}ra{\rm{d}}/s\)
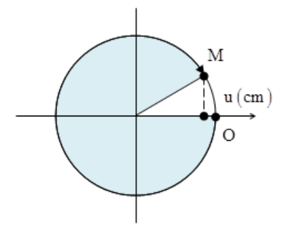
Độ lệch pha dao động theo tọa độ x của M và điểm O : \(\Delta \varphi = \dfrac{{2\pi x}}{\lambda } = \dfrac{{2\pi \dfrac{{11}}{3}}}{4} = \dfrac{{11\pi }}{6}\)
Tại \({t_1}\) M chuyển động theo chiều âm do nằm trước đỉnh sóng
Hai thời điểm \({t_1}\) và \({t_2}\) lệch nhau tương ứng một góc \(\omega t = \dfrac{\pi }{4}\) (chú ý rằng M đang chuyển động ngược chiều dương => ta tính lệch về phía trái)
\({v_{max}} = \omega A = \dfrac{\pi }{4}.8 = 2\pi cm/s\)
Tốc độ của M khi đó: \(v = - {v_{{\rm{max}}}}{\rm{cos}}\left( {{{15}^0}} \right) \approx - 2\pi .cos\left( {{{15}^0}} \right) = - 6,06cm/s\)
Hướng dẫn giải:
+ Sử dụng phương pháp đọc đồ thị dao động sóng
+ Sử dụng các công thức: \(T = \dfrac{\lambda }{v};\Delta \varphi = \omega \Delta t\)
+ Sử dụng vòng tròn lượng giác
Câu hỏi khác
- Đề kiểm tra giữa học kì 1 - đề số 02 Lý 12 có lời giải chi tiết
- Kiểm tra giữa học kì 2 - Đề số 1 môn Lý lớp 12 có lời giải
- Đề kiểm tra giữa học kì 2 - đề số 4 Lý 12 có lời giải chi tiết
- Đề kiểm tra giữa học kì 1 - đề số 01 Lý 12 có lời giải chi tiết
- Đề kiểm tra giữa học kì 2 - đề số 3 Lý 12 có lời giải chi tiết
