Câu hỏi:
2 năm trước
Một hình hộp chữ nhật có đường chéo lớn bằng $17cm$ , các kích thước của đáy bằng $9cm$ và $12cm$ . Tính thể tích của hình hộp chữ nhật đó.
Trả lời bởi giáo viên
Đáp án đúng: b
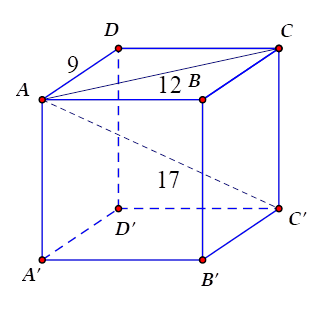
Vì \(ABCD\) là hình chữ nhật nên \(AD = BC = 9\,cm;\,AB = DC = 12\,cm\) .
Áp dụng định lý Pytago cho tam giác vuông \(ADC\) ta được:
\(AC = \sqrt {A{D^2} + D{C^2}} = \sqrt {{{12}^2} + {9^2}} = 15\,cm\)
Ta có \(CC' \bot \left( {ABCD} \right)\) nên \(CC' \bot CD\) .
Áp dụng định lý Pytago cho tam giác vuông \(AC'C\) ta được:
\(CC' = \sqrt {AC{'^2} - A{C^2}} = \sqrt {{{17}^2} - {{15}^2}} = 8\,cm\)
Thể tích của hình hộp chữ nhật bằng
\(9.12.8 = 864\left( {c{m^3}} \right)\)
Hướng dẫn giải:
+ Từ các điều kiện đề bài tìm chiều cao của hình hộp chữ nhật bằng định lý Pytago.
+ Sử dụng công thức thể tích hình hộp chữ nhật để tính toán.
Câu hỏi khác
- Đề kiểm tra 15 phút chương 8: hình lăng trụ đứng. hình chóp đều - đề số 1 Toán 8 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 8: hình lăng trụ đứng. hình chóp đều - đề số 2 Toán 8 có lời giải chi tiết
- Đề kiểm tra 45 phút chương 8: hình lăng trụ đứng. hình chóp đều - đề số 1 Toán 8 có lời giải chi tiết
- Đề kiểm tra 45 phút chương 8: hình lăng trụ đứng. hình chóp đều - đề số 2 Toán 8 có lời giải chi tiết
